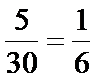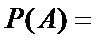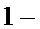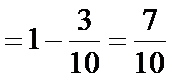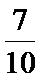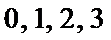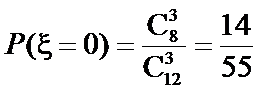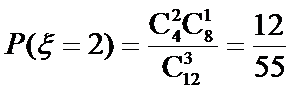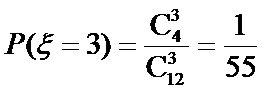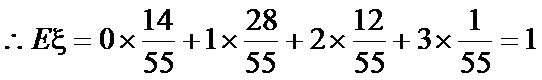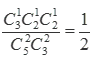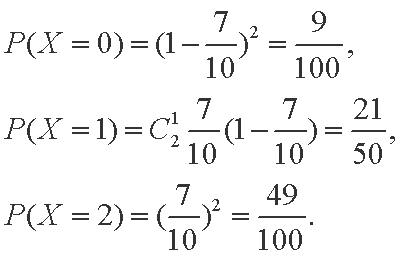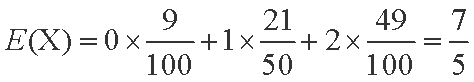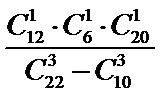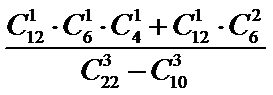- 计数原理
- 共551题
19.设计算法求
正确答案
这是一个累加求和问题,共99项相加,可设计一个计数变量、一个累加变量用循环结构实现这一算法.程序框图如下图所示.
解析
解析已在路上飞奔,马上就到!
知识点
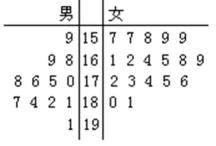
17.第七届城市运动会2011年10月16日在江西南昌举行 ,为了搞好接待工作,运动会组委会在某大学招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”, 身高在175cm以下(不包括175cm)定义为“ 非高个子 ”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”中和“非高个子”中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用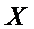
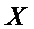
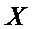
正确答案
(1)根据茎叶图,有“高个子”12人,“非高个子”18人
用分层抽样的方法,每个人被抽中的概率是
所以选中的“高个子”有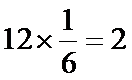
“非高个子”有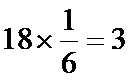
用事件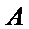
则它的对立事件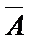
“没有一名“高个子”被选中”
则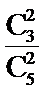
因此,至少有一人是“高个子”的概率是
(2)依题意,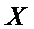
根据茎叶图可知男的高个子有8人,女的有4人;
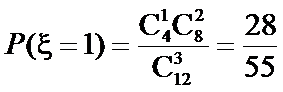
因此,
解析
解析已在路上飞奔,马上就到!
知识点
16.平面几何中,△ABC的内角平分线CE分AB所成线段的比
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
用0,1,2,3,4排成无重复字的五位数,要求偶数字相邻,奇数字也相邻,则该五位数的个数是
正确答案
解析
排除法,偶数字相邻,奇数字也相邻有


知识点
甲、乙两人进行乒乓球比赛,先赢3局者获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次不同视为不同情形)共有( )
正确答案
解析
两人比赛局数为3局、4局或5局.当局数为3时,情况为甲或乙连赢3局,共2种;当局数为4时,若甲胜,则甲第4局胜,且前3局胜2局,有

知识点
某校学生会进行了一次关于“消防安全”的调查活动,组织部分学生干部在几个大型小区随机抽取了50名居民进行问卷调查,活动结束后,团委会对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如下表:
表中所调查的居民年龄在[
(1)求上表中的m,n值,若从年龄在[20,30)的居民中随机选取两人,求这两人至少有一人知道灭火器使用方法的概率;
(2)在被调查的居民中,若从年龄在[10,20),[20,30)的居民中各随机选取2人参加消防知识讲座,记选中的4人中不知道灭火器使用方法的人数为

正确答案
见解析。
解析
(1)由题


记选取的两人至少有一人知道灭火器使用方法为事件A,
则
(2)随机变量
则



所以
所以

知识点
二项式
正确答案
解析
由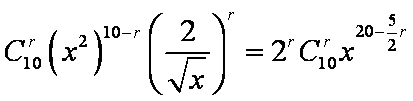
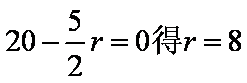

知识点
如果

正确答案
解析
二项展开式的通项为


知识点
甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,现做实验:从这两个箱子里各随机摸出2个球。求:
(1)摸出3个白球的概率;
(2)摸出至少两个白球的概率;
(3)若将摸出至少两个白球记为1分,否则记为0分,则一个人有放回地进行2次上述实验。求此人得分X的分布列及数学期望。
正确答案
见解析
解析
(1)设“在1次游戏中摸出i个白球”为事件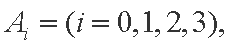
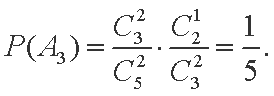
(2)设“至少两个白球”为事件B,则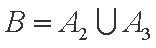
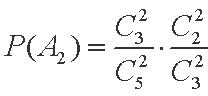
且A2,A3互斥,所以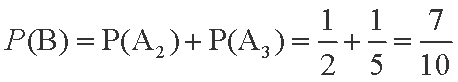
(3) X的所有可能取值为0,1,2.
所以X的分布列是
X的数学期望
知识点
7. 将A,B,C,D,E五种不同的文件放入编号依次为1,2,3,4, 5,6,7的七个抽屉内,每个抽屉至多放一种文件,若文件A、B必须放入相邻的抽屉内,文件C、D也必须放在相邻的抽屉内,则所有不同的放法有 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.有三种卡片分别写有数字1,10和100。设m为正整数,从上述三种卡片中选取若干张,使得这些卡片上的数字之和为m。考虑不同的选法种数,例如当m=11时,有如下两种选法:“一张卡片写有1,另一张卡片写有10”或“11张写有1的卡片”,则选法种数为2。
(1)若m=100,直接写出选法种数;
(2)设n为正整数,记所选卡片的数字和为100n的选法种数为an 当n≥2时,求数列{an}的通项公式。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数f(x)对于任意的正实数x,y,都有f(xy)=f(x)+f(y),若f(2)>0,则下列结论中不正确的是( ).
正确答案
解析
取对数函数模型,
因为f(2)>0,
所以可取f(x)=lg x,
验证可知A,C,D均正确,B错.
故选B.
知识点
10. 某学校4位同学参加数学知识竞赛,竞赛规则规定:每位同学必须从甲、乙两道题中任选一题作答,选甲题答对得30分,答错得-30分;选乙题答对得10分,答错得-10分.若4位同学的总分为0,则这4位同学不同得分情况的种数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.某高中数学老师从一张测试卷的12道选择题、4道填空题、6道解答题中任取3道题作分析,则在取到选择题时解答题也取到的概率为( )
正确答案
解析
从12道选择题、4道填空题、6道解答题中任取3道题取到选择题才取法有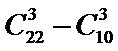
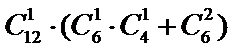
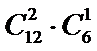
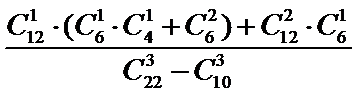
考查方向
解题思路
1.先求任选3道题,取到选择题的解法有多少种;
2.然后求任选的3道题中既有选择题又有解答题的选法有多少种,最后带到古典概型的概率公式中即可。
易错点
1.分类不全,分类没有明确的标准,分类重复等;
2.对于各类情况的算法出错。
知识点
关于从业人员与客户关系协调处理的原则,下列说法正确的是( )。
A.从业人员应当履行对客户尽职调查的义务
B.从业人员在接洽业务过程中,应当衣着得体、态度稳重、礼貌周到
C.从业人员应当耐心、礼貌、认真处理客户的投诉
D.从业人员可以任意收、送客户一些昂贵的礼物
E.从业人员应当根据监管规定要求,对所推荐的产品及服务涉及的法律风险、政策风险以及市场风险等进行充分的提示
正确答案
A,B,C,E
解析
[解析] 在政策法律及商业习惯允许范围内的礼物收、送,应当确保其价值不超过法规和所在机构规定允许的范围。选项D说法有误。
扫码查看完整答案与解析