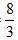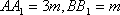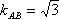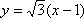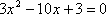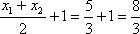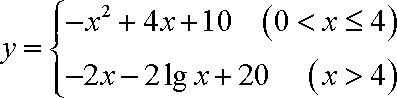计数原理_章节学习

1

题型：单选题

|

单选题 · 5 分

设复数z满足(1－i)z＝2i，则z＝(　　)。

A－1＋i

B－1－I

C1＋i

D1－i

正确答案

A

解析

＝＝－1＋i

知识点

组合数公式的推导

1

题型：填空题

|

填空题 · 5 分

在实数集R中定义一种运算“△”，且对任意，具有性质：

①；②；③ ，

则函数的最小值为。

正确答案

3

解析

略。

知识点

组合数公式的推导

1

题型：简答题

|

简答题 · 13 分

已知，函数，.

（1）求函数的单调区间；

（2）求证：对于任意的，都有.

正确答案

见解析

解析

（1）函数的定义域为,，

因为，所以，当，或时，；

当时，。

所以，的单调递增区间为,单调递减区间为,，……6分

（2）因为在区间上单调递增，在区间上单调递减，

又，，

所以，当时，。

由，可得。

所以当时，函数在区间上是增函数，

所以，当时，。

所以，当时，

对于任意的，都有，，所以。

当时，函数在区间上是增函数，在区间上是减函数，

所以，当时，。

所以，当时，

对于任意的，都有，，所以。

综上，对于任意的，都有， ……………13分

知识点

组合数公式的推导

1

题型：填空题

|

填空题 · 5 分

已知以F为焦点的抛物线上的两点A、B满足,则弦AB的中点到准线的距离为___________.

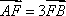
正确答案

解析

设BF=m,由抛物线的定义知

中，AC=2m,AB=4m,

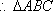
直线AB方程为

与抛物线方程联立消y得

所以AB中点到准线距离为

知识点

组合数公式的推导

1

题型：单选题

|

单选题 · 5 分

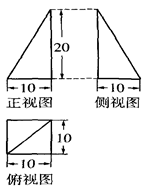
某师傅用铁皮制作一封闭的工件，其直观图的三视图如右图示

（单位长度：cm，图中水平线与竖线垂直），则制作该工件用去的

铁皮的面积为( )cm2，（制作过程铁皮的损耗和厚度忽略不计）

A500

B100 (3+√5)

C100 (3+√6)

D600

正确答案

B

解析

略

知识点

组合数公式的推导

1

题型：填空题

|

填空题 · 5 分

2个好朋友一起去一家公司应聘，公司人事主管通知他们面试时间时说：“我们公司要从面试的人中招3个人，你们都被招聘进来的概率是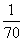” 。根据他的话可推断去面试的人有______个（用数字作答）。

正确答案

21

解析

略

知识点

组合数公式的推导

1

题型：单选题

|

单选题 · 5 分

小明有4枚完全相同的硬币，每个硬币都分正反两面.他想把4个硬币摆成一摞,且满足相邻两枚硬币的正面与正面不相对,不同的摆法有（）

A4种

B5种

C6种

D9种

正确答案

B

解析

略

知识点

组合数公式的推导

1

题型：填空题

|

填空题 · 5 分

某小区有7个连在一起的车位，现有3辆不同型号的车

需要停放，如果要求剩余的4个车位连在一起，那么

不同的停放方法共有 __________种。（用数字作答）

正确答案

24

解析

略

知识点

组合数公式的推导

1

题型：简答题

|

简答题 · 13 分

为了解甲、乙两个快递公司的工作状况，假设同一个公司快递员的工作状况基本相同，现从甲、乙两公司各随机抽取一名快递员，并从两人某月（30天）的快递件数记录结果中随机抽取10天的数据，制表如下：

每名快递员完成一件货物投递可获得的劳务费情况如下：

甲公司规定每件4.5元；乙公司规定每天35件以内（含35件）的部分每件4元，超出35件的部分每件7元.

（1）根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数；

（2）为了解乙公司员工B的每天所得劳务费的情况，从这10天中随机抽取1天，他所得的劳务费记为（单位：元），求的分布列和数学期望；

（3）根据表中数据估算两公司的每位员工在该月所得的劳务费。

正确答案

见解析

解析

（1）甲公司员工A投递快递件数的平均数为36，众数为33. ------------------------2分

（2）设为乙公司员工B投递件数，则

当=34时，=136元，当>35时，元，

的可能取值为136,147,154,189,203 ---------------------------4分

{说明：X取值都对给4分，若计算有错，在4分基础上错1个扣1分，4分扣完为止}

的分布列为：

---------------------------------9分

{说明：每个概率值给1分，不化简不扣分，随机变量值计算错误的此处不再重复扣分}

---------------------------------11分

（3）根据图中数据，可估算甲公司被抽取员工该月收入4860元，乙公司被抽取员工该月收入4965元. ---------------------------------13分

知识点

组合数公式的推导

1

题型：单选题

|

单选题 · 5 分

在复平面内，复数（是虚数单位）对应的点在

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

B

解析

略

知识点

组合数公式的推导

1

题型：填空题

|

填空题 · 5 分

二项式的展开式中，常数项是 .

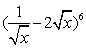
正确答案

-160

解析

略

知识点

组合数公式的推导

1

题型：单选题

|

单选题 · 5 分

某岗位安排3名职工从周一到周五值班，每天只安排一名职工值班，每人至少安排一天，至多安排两天，且这两天必须相邻，那么不同的安排方法有（）

A10种

B12种

C18种

D36种

正确答案

C

解析

略

知识点

组合数公式的推导

1

题型：单选题

|

单选题 · 5 分

设的展开式中的常数项为，则直线与曲线围成图形的面积为

A

B9

C

D

正确答案

C

解析

∵的展开式中的常数项为,即.

解得或，由定积分的几何意义知，直线与曲线围成图形的面积为=.选C.

知识点

组合数公式的推导

1

题型：单选题

|

单选题 · 5 分

在的展开式中，的系数为（）

A-25

B45

C-55

D25

正确答案

C

解析

略

知识点

组合数公式的推导

1

题型：简答题

|

简答题 · 15 分

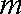
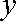
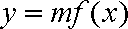
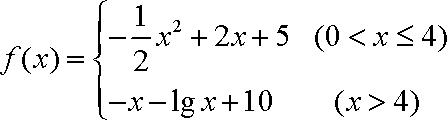
某药厂在动物体内进行新药试验，已知每投放剂量为的药剂后，经过小时该药剂在动物体内释放的浓度(毫克/升) 满足函数，其中，当药剂在动物体内中释放的浓度不低于(毫克/升)时，称为该药剂达到有效。

（1）若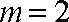，试问该药达到有效时，一共可持续多少小时（取整数小时）?

（2）为了使在8小时之内（从投放药剂算起包括8小时）达到有效，求应该投放的药剂量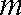的最小值（取整数）。

正确答案

见解析

解析

（1）时，

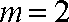
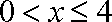
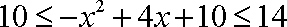
当时，，显然符合题意（2分）

当时，通过计算器由解得：（4分）

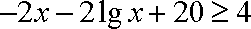
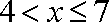
综上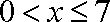，所以该药剂达到有效时，一共可持续7小时. （6分）

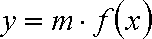
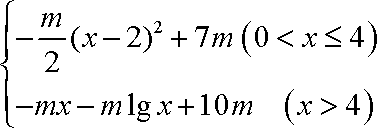
（2）由= （8分）

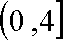
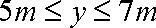
可知在区间上有，即，

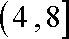
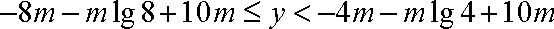
在区间上单调递减，即，（10分）

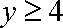
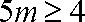
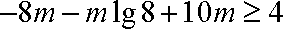
为使恒成立，只要且（12分）

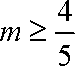
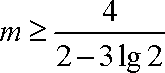
即且，求得：.

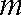
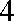
答：为了使在8小时之内达到有效，投放的药剂剂量的最小值为，（15分）

知识点

组合数公式的推导

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点