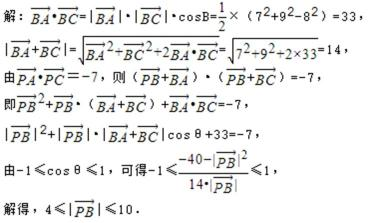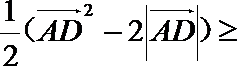- 平面向量
- 共1314题
5.已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若向量a,b的夹角为150°,



正确答案
解析
由于<a,b>=150°,





知识点
6.已知直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.有一列向量






正确答案

解析
由题可知,差向量为(1,1),则向量an=(-21+n,12+n)。所以|an|2=(-21+n)2+(12+n)2=2n2-18n+585,则当n=4或5时取到最小值。
考查方向
本题主要考查了向量的模及新定义。
解题思路
本题考查向量的模,按照定义求解。
易错点
本题要注意按照定义求解。
知识点
11.若向量a,b满足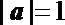
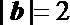
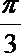
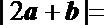
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知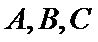
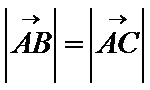
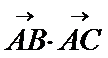
正确答案
解析
1.设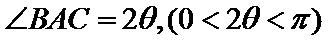
则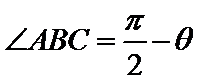
则
所以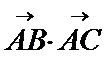
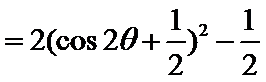
所以当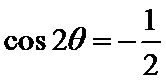
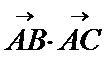
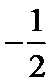
考查方向
易错点
1.不能正确引入变量表示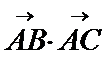
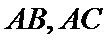
知识点
3.已知向量



正确答案
解析
由


考查方向
本题主要考查了向量的垂直与模——向量的数量积运算,在近几年的各省高考题出现的频率较高,常单独命题或与解三角形、三角函数等知识点结合。
易错点
本题易在数量积运算上出错。
知识点
向量






正确答案
解析
由已知,得对




考查方向
本题主要考查了向量模的概念以及数量积的运算能力,也是常考题型
易错点
向量模的运算以及数量积的运算能力
知识点
13.向量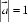
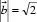
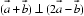

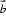
正确答案
解析
由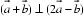
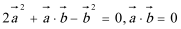

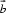
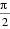
考查方向
本题主要考查了平面向量的夹角公式。
解题思路
本题考查平面向量的夹角公式,解题步骤如下:
1、利用垂直条件求出数量积。
2、利用夹角公式求解.
易错点
本题必须注意数量积的公式。
知识点
3.平面向量
正确答案
解析




考查方向
本题主要考查两个向量的数量积的定义,求向量的模的方法,属于中档题
解题思路
先求出
易错点
数量积表示两个向量的夹角,向量的模
知识点
8.已知向量 的夹角为

正确答案
解析
∵
∴


考查方向
解题思路
依题意

易错点
本题易在
知识点
13.已知

正确答案
.
解析


考查方向
解题思路
1.先根据向量

易错点
运算会出错或不会求向量
知识点
16.已知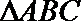
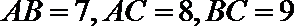
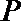
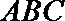
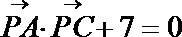
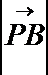
正确答案
10
解析
考查方向
本题主要考查了解三角形和平面向量及不等式
解题思路
本题考查解三角形和平面向量及不等式,解题思路如下:1、利用公式表示数量积;2、利用不等式求解。
易错点
本题必须注意数量积公式
知识点
16. 设



正确答案
解析

由余弦函数的单调性可知
因为
所以“

考查方向
解题思路
本题考查平面向量的基础知识,直接运算即可。把条件判断转化为集合关系的判断更有利于解题。
易错点
本题必须注意充要条件的判定的方向性,A是B的XX条件和A的XX条件是B要区分清楚,忽视则会出现错误。
知识点
11.已知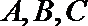
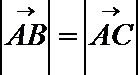
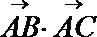
正确答案
解析
设: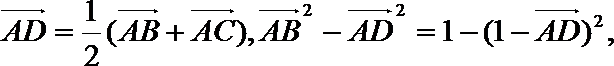
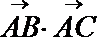
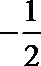
考查方向
本题主要考查平面向量
解题思路
1、在单位圆中表示出向量;
2、利用圆的性质求解,即可得到结果。A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在化简时发生错误。
知识点
扫码查看完整答案与解析