- 平面向量
- 共1314题
3.设向量


正确答案
解析
因为,向量
所以,此题选B
考查方向
平面向量的数量积的运算
解题思路
根据向量垂直,向量的模的概念和性质计算求解
易错点
计算错误,不会求向量的数量积
教师点评
要掌握向量的相关恒等变形,化简后求值
知识点
已知向量


17.求向量

18.求
正确答案
解析
∵
又
∴
即
解得
又
所以

考查方向
解题思路
由题意,可根据题中条件求出
的夹角;
易错点
要区分点的坐标和向量的坐标,向量坐标中包含向量大小和方向两种信息;两个向量共线有方向相同、相反两种情况。
正确答案
解析

考查方向
解题思路
先对
易错点
求向量模的常用方法:利用公式
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设图一是某几何体的三视图,则该几何体的体积为( )
正确答案
解析
有三视图可知该几何体是一个长方体和球构成的组合体,其体积
知识点
椭圆C:
正确答案
解析
设P点坐标为(x0,y0),则



故
∵
∴
知识点
若集合


正确答案
解析
根据集合A 



知识点
某几何体三视图如图所示,则该几何体的体积为
正确答案
解析
由三视图知:几何体是正方体切去两个
正方体的棱长为2,切去的圆柱的底面半径为1,高为2,
∴几何体的体积V=23﹣2×
知识点
在等差数列{an}中,a1+a3=8,且a4为a2和a9的等比中项,求数列{an}的首项、公差及前n项和。
正确答案
数列{an}的首项为4,公差为0,或首项为1,公差为3.
数列的前n项和Sn=4n或Sn=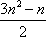
解析
设该数列公差为d,前n项和为Sn.
由已知,可得2a1+2d=8,(a1+3d)2=(a1+d)(a1+8d)。
所以,a1+d=4,d(d-3a1)=0,解得a1=4,d=0,或a1=1,d=3,即数列{an}的首项为4,公差为0,或首项为1,公差为3.
所以,数列的前n项和Sn=4n或Sn=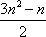
知识点
根据如图所示的伪代码,当输入a,b分别为2,3时,最后输出的m的值为________.
正确答案
3
解析
由已知可知,m为a,b中的最大值,故最后输出的m值为3.
知识点
如图,在平面直角坐标系xOy中,M,N分别是椭圆

(1)若直线PA平分线段MN,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意的k>0,求证:PA⊥PB.
正确答案
见解析
解析
(1)由题设知,a=2,b=




(2)直线PA的方程为y=2x,代入椭圆方程得




于是C


因此,
(3)解法一:将直线PA的方程y=kx代入



故直线AB的斜率为

解得

于是直线PB的斜率
因此k1k=-1,所以PA⊥PB.
解法二:设P(x1,y1),B(x2,y2),则x1>0,x2>0,x1≠x2,A(-x1,-y1),C(x1,0).设直线PB,AB的斜率分别为k1,k2.因为C在直线AB上,所以
因此k1k=-1,所以PA⊥PB.
知识点
若集合

正确答案
解析

知识点
已知f(x)=m(x-2m)(x+m+3),g(x)=
①
②
则m的取值范围是
正确答案
解析
根据


































知识点
扫码查看完整答案与解析












































