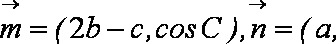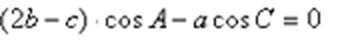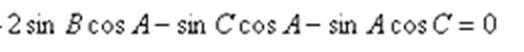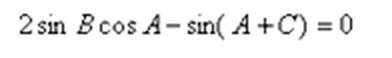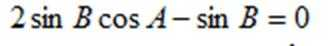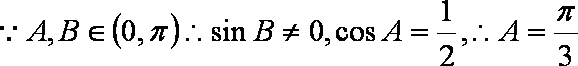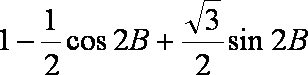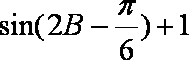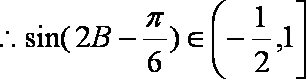- 平面向量
- 共1314题
设函数f(x)=(x﹣1)2+blnx,其中b为常数。
(1)当
(2)若函数f(x)的有极值点,求b的取值范围及f(x)的极值点;
(3)求证对任意不小于3的正整数n,不等式
正确答案
见解析。
解析
(1)由题意知,f(x)的定义域为(0,+∞),
∴当
(2)①由(Ⅰ)得,当
②



∴
③当
∴(i)b≤0时,

此时f'(x),f(x)随x在定义域上的变化情况如表:
由
此表可知:∵b≤0时,f(x)有惟一极小值点
(ii)当
此时,f'(x),f(x)随x的变化情况如下表:
由此表可知:


综上所述:当且仅当
当b≤0时,f(x)有惟一最小值点
当

(3)由(2)可知当b=﹣1时,函数f(x)=(x﹣1)2﹣lnx,
此时f(x)有惟一极小值点
且
令函数h(x)=(x﹣1)﹣lnx(x>0)
知识点
如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且

正确答案
解析
略
知识点
已知向量





正确答案
解析


∴

知识点
已知






(1)求
(2)若存在一条与




(3)当实数

正确答案
见解析。
解析
(1)



关于


也就是不等式

∴


由韦达定理得:
∴
(2)由(1)得








令
当



从而

(3)

∴
方程

①若

或
则



∴函数


此时函数


②若






此时

下面只需考虑
由


当
故

∴函数

∴函数
当
则





∴函数



此时函数


综上所述, 若



若






知识点
随机变量ξ服从正态分布N(40, 
正确答案
0.6
解析

所以
知识点
非零向量




正确答案
解析
略
知识点
已知向量




(1)求向量
(2)若向量









正确答案
(1)
解析
(1)设


又向量



由①、②解得



(2)向量


由





得


知识点
若



正确答案
解析
因为







知识点
已知向量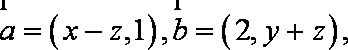

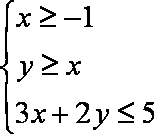
正确答案
解析
由

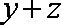
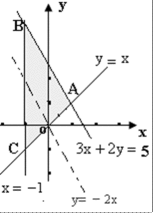
画出不等式组的可行域,如右图,目标函数变为: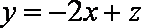
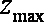
知识点
在△ABC中,∠A=90°,AB=1,AC=2,设点P,Q满足

正确答案
解析
由题意可得

由于




=0﹣(1﹣λ)

解得 λ=
故答案为:
知识点
已知非零向量




正确答案
解析
因为向量






知识点
已知向量



正确答案
解析
因为向量




知识点
在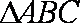
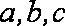
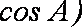
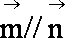
(1)求角A的大小;
(2)求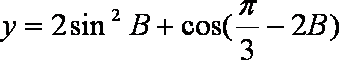
正确答案
见解析
解析
(1)由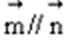
由正弦定理得
(2)
=
=
由(1)得
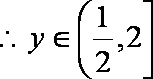
知识点
设m、n是两条不同的直线,

正确答案
解析
因为两直线与同一平面平行,两直线位置关系不定,所以选项A错误.当直线平行于两相交平面的交线时,该直线与两平面皆平行,所以选项B错误.同样理由可得:选项D错误.当 m





知识点
在

(1)求
(2)求
正确答案
(1)
解析
(1)因为
(2)
所以

知识点
扫码查看完整答案与解析