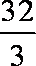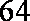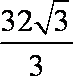- 平面向量
- 共1314题
已知向量


(1)求

(2)在△ABC中,




正确答案
见解析。
解析
(1)

由


因为




(2)根据题意


因为

因为

根据余弦定理

所以

知识点
已知向量a,b满足a=(-2 sinx,



(1)将


(2)已知数列

正确答案
见解析。
解析
(1)
(2)
所以
又
所以
知识点
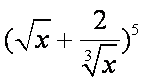
正确答案
80
解析
略
知识点
已知F1,F2分别是双曲线



正确答案
解析
由双曲线方程
由抛物线方程


由
又双曲线左准线为
∴
故选B
知识点
如图,AB为圆




(1)求证:

(2)求证:CD2=CF·CP。
正确答案
见解析
解析
解析:证明:(1) 





(2)在




∴
知识点
为迎接建党90周年,某班开展了一次“党史知 识竞赛”,竞赛分初赛和决赛两个阶段进行,在初赛后,把成绩(满分为100分,分数均为整数)进行统计,制成如右图的频率分布表:
(1)求
(2)决赛规则如下:为每位参加决赛的选手准备四道题目,选手对其依次作答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对一道,则获得二等奖.某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于90分的频率的值相同.设该同学决赛中答题个数为X,求X的分布列以及X的数学期望。
正确答案
见解析
解析
(1)
(2)X的可能取值为2,3,4

所以分布列为
知识点
已知函数f(x)=



(1)讨论函数
(2)若


若首项

若首项为正整数,数列
正确答案
见解析
解析
解(1)可知


当




当







此时


当




综上,当












(2)若






因为


假设




所以,由数学归纳法可得

(2)由(1)知:当且仅当

所以,题设即


由



令








知识点
已知=(c,0)(c>0), =(n,n)(n∈R), ||的最小值为1,若动点P同时满足下列三个条件:
①|| = ||(a>c>0);
② =

③动点P的轨迹C经过点B(0,-1) 。
(1)求c的值;
(2)求曲线C的方程;
(3)是否存在方向向量为a=(1,k)(k≠0)的直线l,使l与曲线C交于两个不同的点M、N,且||=||?若存在,求出k的范围;若不存在,请说明理由。
正确答案
见解析。
解析
(1)法一: 
当n= 

法二:设G(x,y),则G在直线y=x上,所以

(2)∵



∴点P在以F为焦点, 
设P(x,y), 则有

∴曲线C的方程为
(3)假设存在方向向量为a0=(1,k)(k≠0)的直线l满足条件,则可设l:y=kx+m(k≠0),
与椭圆
由判别式△>0,可得m2<3k2+1. ①
设M(x1,y1),N(x2,y2), MN的中点P(x0,y0),由|BM|=|BN|, 则有BP⊥MN.
由韦达定理代入kBP= 

联立①②,可得到 k2-1<0,
∵k≠0, ∴ -1<k<0或0<k1.
即存在k∈(-1,0)∪(0,1),使l与曲线C交于两个不同的点M、N,且
知识点
如图所示, 








(1) 求证
(2) 求
正确答案
见解析
解析
解析:(1)∵ 





(2)
∵




又由(1)知




知识点
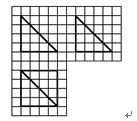
7.如图,网格纸上小正方形的边长为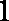
正确答案
解析
由三视图可知,该多面体是一个四棱锥,且由一个顶点出发的三条侧棱两两垂直,长度都为4, ∴其体积为
知识点
21.设动点




(1)求点
(2)设圆








正确答案
(1)依题意知,
动点



曲线

∵ 
∴ 曲线
(2)设圆的圆心为
∵ 圆

∴ 圆的方程为
令
设圆与

方法1:不妨设

∴
又∵点


∴ 

∴当

方法2:∵
∴
又∵点

∴ 

∴当

解析
解析已在路上飞奔,马上就到!
知识点
12.已知点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正确答案
D
解析
略
知识点
1.满足M
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 若



正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析