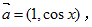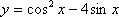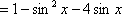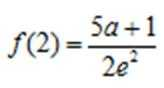- 平面向量
- 共1314题
若向量

正确答案
解析
略
知识点
已知集合







(1)当




(2)(ⅰ)证明:若



(ⅱ)设



说明理由;
(3)记




正确答案
见解析
解析
(1)解:当

得 

由 


(2)(ⅰ)证明:设


因为 

所以 

即 


所以 

所以

(ⅱ)解:设



反例如下:取


则 



因为

所以不存在

(3)解法一:因为 
设






所以
因为 
所以 

所以 
因为

又 
所以

即 
对于 





综上,

解法二:首先证明如下引理:设

证明:因为 

所以 
即 
所以

上式等号成立的条件为


对于 





综上,

知识点
在






正确答案
解析
略
知识点
已知圆O的半径为R (R为常数),它的内接三角形ABC满足


正确答案
见解析
解析
由
由正弦定理得


所以
=
当且仅当

知识点
已知向量






正确答案
解析


知识点
已知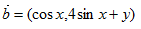
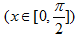
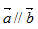
正确答案
解析
由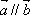
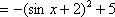
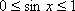
知识点
设向量


正确答案
解析
略
知识点
已知点



正确答案
解析


知识点
若

正确答案
见解析。
解析
因为18=6×3=[(1+2x)+(3+x)+(2﹣3x)](1+1+1),
由柯西不等式可得:
又
所以
知识点
过双曲线






正确答案
解析
设双曲线的右焦点为A,则












知识点
若点





(1)求证:
(2)若点


值; 若不存在,请说明理由.
正确答案
见解析
解析
解:(1)因为点

所以


若直线



若直线




有
那么,
(2) 若直线


若直线
点





则
知识点
已知在直角坐标系



极点,

(1)求直线

(2)设点



正确答案
见解析
解析
(1)直线

曲线的直角坐标方程为
(2)设点
所以

知识点
已知定义域为

(1)求
(2)解关于

正确答案
(1)a=2,b=1(2)
解析
(1)因为



(2) 由(1)知
由上式易知

又因

因

即
知识点
设等差数列





则
正确答案
解析
第一步识别条件:等差数列;头脑中闪过等差数列的种种公式
继续识别条件:



第二步转化条件:可以求出来啊,这个方程不是白给的吗?一个 2,一个-1
第三步看问定向: 
第四步结论已出现:5/2
知识点
设a∈R,函数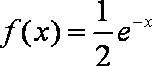

(1) 判断函数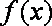
(2) 当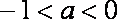
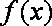
正确答案
(1)区间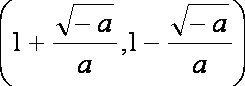
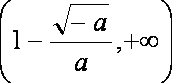
(2)
解析
(1)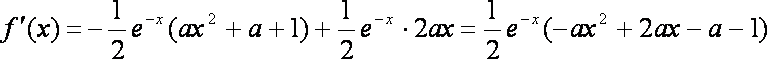
由于
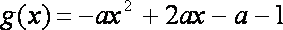
当a = 0时, 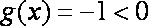
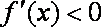
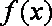
当a>0时, 由于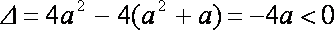
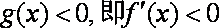
函数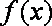
当a<0时, 解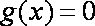
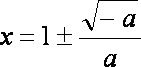
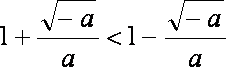
在区间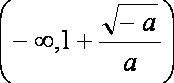
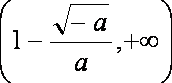
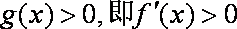
函数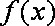
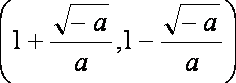
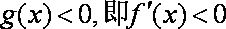
函数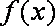
综上可知:当a≥0时,函数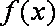
函数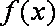
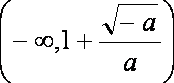

在区间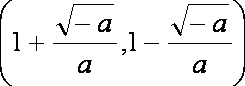
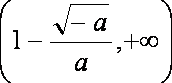
(2) 当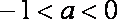
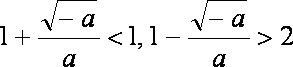
所以, 函数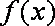
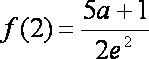
知识点
扫码查看完整答案与解析