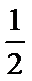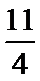- 平面向量
- 共1314题
在△ABC中，角A，B，C的对边分别为a，b，c，向量
16．求角
17.若a＝6，求△ABC面积的最大值．
正确答案
（Ⅰ）
解析
试题分析：本题属于三角函数的基本问题，题目的难度是逐渐由易到难，（1）直接按步骤来求解，（2）要注意注明基本不等式等号成立的条件.
（Ⅰ）因为向量
所以
由正弦定理得
即
由于B是三角形的内角，
则
考查方向
解题思路
本题考查平面向量共线的坐标表示、解三角形，解题步骤如下：
1）利用平面向量共线的坐标表示得到三角形的边角关系；
2）利用正弦定理将边角关系转化为角角关系，利用三角形的内角和定理进行求解；
3）利用余弦定理得到边边关系；
4）利用基本不等式和三角形的面积公式进行求解。
易错点
1）易混淆平面向量共线的坐标表示与垂直的坐标表示；
2）利用基本不等式求最值时，忽视注明等号成立的条件.
正确答案
（Ⅱ）
解析
试题分析：本题属于三角函数的基本问题，题目的难度是逐渐由易到难，（1）直接按步骤来求解，（2）要注意注明基本不等式等号成立的条件.
（Ⅱ）因为
所以
且仅当b=c时取得等号，所以
故
所以当b＝c时，
考查方向
解题思路
本题考查平面向量共线的坐标表示、解三角形，解题步骤如下：
1）利用平面向量共线的坐标表示得到三角形的边角关系；
2）利用正弦定理将边角关系转化为角角关系，利用三角形的内角和定理进行求解；
3）利用余弦定理得到边边关系；
4）利用基本不等式和三角形的面积公式进行求解。
易错点
1）易混淆平面向量共线的坐标表示与垂直的坐标表示；
2）利用基本不等式求最值时，忽视注明等号成立的条件.
已知平面向量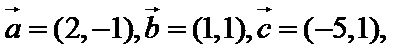
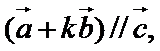
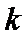
A2
B
C
D
正确答案
解析
由
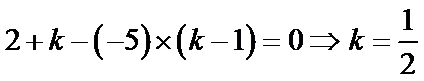
考查方向
解题思路
由
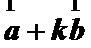
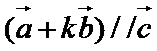
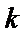
易错点
本题易在坐标运算上出错。
知识点
正确答案
ＬＵＥ
知识点
正确答案
略
知识点
10.若向量a
Aa与b的夹角等于
B(a+b)⊥(a-b)
Ca∥b
Da⊥b
正确答案
解析
∵角
∵当
∵
∴
故选B.
考查方向
解题思路
此题中的
易错点
利用向量平行或垂直来解决解析几何中的平行和垂直问题可以不用讨论斜率不存在的情况，要注意：
(1)
（2）
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图，正六边形ABCDEF中，
A
B
C
D
正确答案
解析
知识点
填空题：本大题共4小题，每小题5分。
13.设向量
正确答案
试题分析：因为向量
解析
解析已在路上飞奔，马上就到！
知识点
17.
（1）求
（2）若
正确答案
（1）因为
由正弦定理，得
又
由于
（2）解法一：由余弦定理，得
而
得
因为
故
解法二：又正弦定理，得
从而
又由
故
所以
解析
解析已在路上飞奔，马上就到！
知识点
集合{－1,0,1}共有__________个子集。
正确答案
8
解析
由于集合{－1,0,1}有3个元素，故其子集个数为23＝8.
知识点
若向量
A
B
C
D
正确答案
解析
略
知识点
执行如图3所示的程序框图，如果输入
正确答案
9
解析
略
知识点
如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，正方体的六个面所在的平面与直线CE，EF相交的平面个数分别记为m，n，那么m＋n＝( )。
正确答案
解析
由CE与AB共面，且与正方体的上底面平行，则与CE相交的平面个数m＝4.作FO⊥底面CED，一定有面EOF平行于正方体的左、右侧面，即FE平行于正方体的左、右侧面，所以n＝4，m＋n＝8.故选A
知识点
已知变量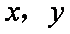
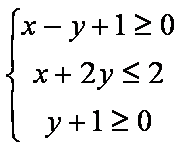
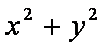
正确答案
17
解析
由题设可得，点（0，0）在可行域内，故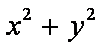
时，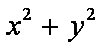
知识点
扫码查看完整答案与解析