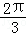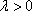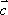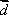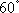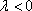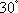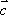- 平面向量
- 共1314题
设向量


已知向量






正确答案
解析
略
知识点
已知



正确答案
解析
:由题意知 λ

又因为两向量垂直,
所以(-3λ﹣1,2λ)(﹣1,2)=0,即3λ+1+4λ=0,
解得λ=
故选A。
知识点
如图,平行四边形ABCD中,AB=2,AD=1,∠A=60°,点M在AB边上,且

正确答案
解析
略
知识点
已知向量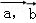
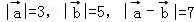
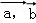
正确答案
解析
解:∵|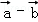
∴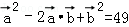
∴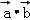
∴cos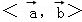
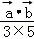
∵θ∈[0,π]
∴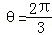
故答案为:
知识点
设


正确答案
解析
由柯西不等式,

知识点
已知向量



正确答案
解析
略
知识点
在平面直角坐标系中,若点
















正确答案
1,
解析
略
知识点
设


正确答案
解析
略
知识点
已知平面向量




正确答案
解析
略
知识点
已知向量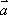
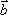
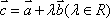
向量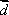
正确答案
解析
先将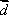

判断A、将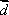
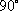
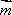
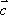
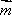
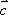
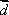
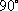
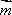
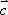
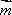
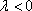
选项B,C,D推理同上,注意用方格判断

知识点
己知



正确答案
见解析。
解析
∵


当m=l时,
当m>l时,
知识点
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD
(1)求证:BM∥平面ADEF:
(2)求直线DB与平面BEC所成角的正弦值;
(3)求平面BEC与平面DEC所成锐二面角的余弦值.
正确答案
解析
证明 :(1)取DE中点N,连结MN,aN
在
所以MN//CD,且
又已知AB//CD,且
所以四边形ABMN为平行四边形 ,所以BM//AN
又因为

所以MM//平面ADEF
(2)解:在矩形ADEF中,ED⊥AD,又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD,又AD⊥CD,
所以,取D为原点,DA、DC、DE所在直线分别为x,y,z轴,建立直角坐标系,则
D(0,0,0),B(1,1,0),C(0,2,0),E(0,0,3)
设
因为

所以


设DB与平面BEC所成角为α,则
sinα=|cos

所以,DB与平面BEC所成角的正弦值为
(3)易证DA⊥平面DEC,取
设平面BEC与平面DEC所成锐二面角为
cos

所以,平面BEC与平面DEC所成锐二面角的余弦值为
知识点
在本次考试中共有12道选择题,每道选择题有4个选项,其中只有一个是正确的,得分标准规定:“每题只选一项,答对得5分,不答或答错得0分”,某考生每道题都给出一个答案,该考生已确定有9道题的答案是正确的,而其余题中,有1道题可判断出两个选项是错误的,有一道可以判断出一个选项是错误的,还有一道因不了解题意只能乱猜,试求该考生
(1)选择题得60分的概率;
(2)选择题所得分数
正确答案
见解析
解析
(1)设得分为60分为事件
得分为60分,12道题必须全做对,在其余的3道题中,有1道题答对的概率为


所以得分为60分的概率为
(2)依题意,该考生得分
得分为45分表示只做对了9道题,其余各题都做错,
所以概率为
得分为50分的概率为
得分为55分的概率为
得分为60分的概率为
所以得分
数学期望
知识点
设x,y∈R,向量








正确答案
解析
∵ 向量






解得 x=2,y=﹣2,故
故有|


故选B。
知识点
极坐标系与直角坐标系











(1)求证:
(2)当




正确答案
见解析
解析
解(1)设点
∵点

则


(2)由曲线



当
化为直角坐标为

∵直线斜率为

直线BC的普通方程为
∵过点


知识点
扫码查看完整答案与解析