- 平面向量
- 共1314题
14.已知向量


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
4. 点
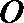
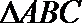
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 关于平面向量的命题
①







②如




③




④





其中正确命题个数有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.关于平面向量a,b,c,有下列三个命题:
①若a·b=a·c,则b=c.
②若a=(1,k),b=(-2,6),a∥b,则k=-3.
③非零向量a和b满足|a|=|b|=|a-b|,则a与a+b的夹角为60°.
其中真命题的序号为______.(写出所有真命题的序号)
正确答案
②
解析
解析已在路上飞奔,马上就到!
知识点
3.若向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知向量


(1)若



(2)若



正确答案
(1)当

所以 

(2)
因为
当


当


所以
解析
解析已在路上飞奔,马上就到!
知识点
15. 在三棱锥P-ABC中,给出下列四个命题:
① 如果PA⊥BC,PB⊥AC,那么点P在平面ABC内的射影是△ABC的垂心;
② 如果点P到ABC的三个顶点的距离都相等,那么点P在平面ABC内的射影是△ABC的内心;
③ 如果棱PA和BC所成的角为60o,PA=BC=2,E、F分别是棱PB、AC的中点,那么EF=1;
④ 如果三棱锥P-ABC的各棱长均为1,则该三棱锥在任意一个平面内的正投影(投影线垂直投影面)的面积都不大于;
其中正确命题的序号是____________.
正确答案
①③④
解析
解析已在路上飞奔,马上就到!
知识点
3.已知某随机变量X的概率密度函数为P(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某学校的某一专业从8名优秀毕业生中选派5名支援中国西部开发建设, 其中甲同学必须被选派的概率是______
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.如图所示,在边长为2的正六边形






正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
3. {an}是等比数列,则“a1<a2<a3”是“数列{an}是递增数列”的( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知M={





M
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.称




①
②
③对任意的
则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示。其上部分是以AB为直径的半圆,点O为圆心,下部分是以AB为斜边的等腰直角三角形,DE、DF是两根杆,其中AB=2 m,∠EOA=∠FOB=2x(0<x<)。现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯。若每种灯的“心悦效果”均与相应的线段或弧的长度成比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和。
(1) 试将y表示为x的函数;
(2) 试确定当x取何值时,该霓虹灯整体的“心悦效果”最佳?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设


①若a∥

②若a∥



③若a⊥



④若a、b在平面
其中正确命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析



















