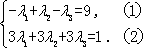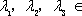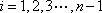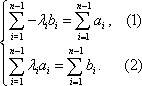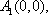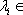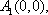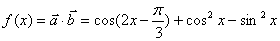- 平面向量
- 共1314题
集合{-1,0,1}共有__________个子集。
正确答案
8
解析
由于集合{-1,0,1}有3个元素,故其子集个数为23=8.
知识点
若向量


正确答案
解析
略
知识点
在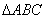
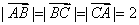
正确答案
解析
知识点
在





正确答案
解析



知识点
执行如图3所示的程序框图,如果输入


正确答案
9
解析
略
知识点
已知双曲线










(1)求实数
(


(3)若点










正确答案
见解析。
解析
(1)解:设双曲线

由题意可得
解得
(2)证明:由(1)可知,直线



因为

所以
因为点



所以

所以直线


(3)证法1:设点









设

即
整理,得
由①×③,②×④得
将

得
将⑤代入⑦,得
所以点

证法2:依题意,直线

设直线

由
消去

因为直线



则有
设点
由

整理得
将②③代入上式得
整理得
因为点


联立④⑤消去

所以点

知识点
已知向量






正确答案
解析
略
知识点
在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)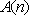
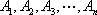
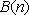
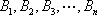

①两点列的起点和终点分别相同;②线段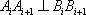
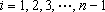
则称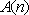
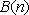
(1)求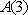
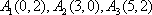
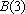
(2)判断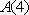
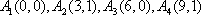
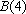
(3)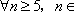
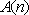
正确答案
见解析
解析
(1)设点列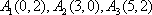

由正交点列的定义可知

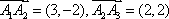
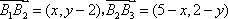
由正交点列的定义可知 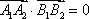
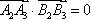
即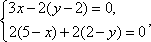
所以点列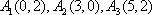
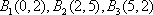
(2)由题可得 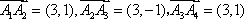
设点列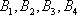
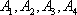
则可设
因为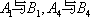
因为
所以有序整点列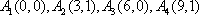
(3)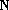
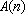

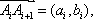

若有序整点列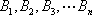
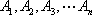
则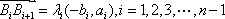
则有
①当

由于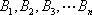

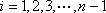
等式(2)中左边是3的倍数,右边等于1,等式不成立,
所以该点列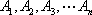
②当
取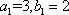

由于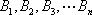

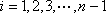
等式(2)中左边是3的倍数,右边等于1,等式不成立,
所以该点列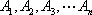
综上所述,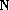
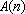
知识点
如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( )。
正确答案
解析
由CE与AB共面,且与正方体的上底面平行,则与CE相交的平面个数m=4.作FO⊥底面CED,一定有面EOF平行于正方体的左、右侧面,即FE平行于正方体的左、右侧面,所以n=4,m+n=8.故选A
知识点
已知变量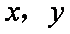
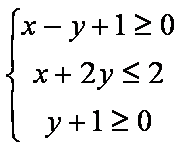
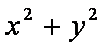
正确答案
17
解析
由题设可得,点(0,0)在可行域内,故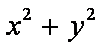
时,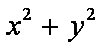
知识点
已知向量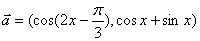
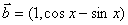
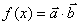
(1)求函数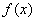
(2)在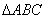
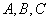
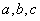

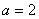
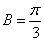
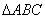
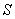
正确答案
见解析。
解析
(1)
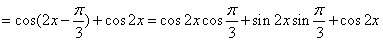
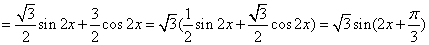
令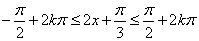
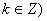
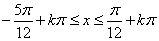
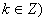
所以,函数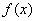
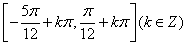
(2)由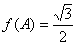
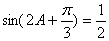
因为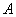
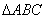
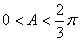
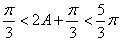
因此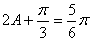
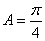
又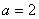

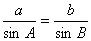
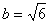
由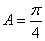
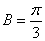
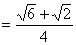
所以,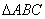
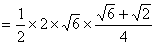
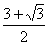
知识点
在平面直角坐标系






正确答案
解析
略
知识点
设









正确答案
2
解析
略
知识点
已知向量





正确答案
解析
由


知识点
在平面直角坐标系xoy中,直线l的参数方程是



正确答案
2
解析
略
知识点
扫码查看完整答案与解析