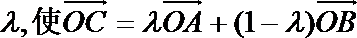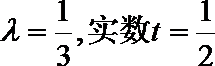- 平面向量
- 共1314题
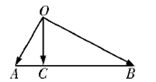
如图所示,点








正确答案
1;
解析
略
知识点
在平面直角坐标系中,O是坐标原点,两定点A,B满足

正确答案
解析
略
知识点
△ABC中,点D在边AB上,CD平分∠ACB,若
正确答案
解析
知识点
如图所示,在边长为2的正六边形






正确答案
5
解析
略
知识点
已知向量


正确答案
4
解析
略
知识点
△ABC中,M为BC上任意一点,N为AM中点,若

正确答案
解析
设M为BC的中点,则

或

知识点
如图,在




正确答案
答案:
解析
略
知识点
设


n 





正确答案
5
解析
∵m







则








知识点
7.已知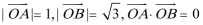

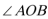
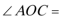

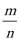
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在∆ABC中,已知D是AB边上一点,若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若




则角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14、在平行四边形ABCD中,E和F分别是边CD和BC的中点,且


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设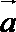
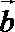
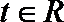
(1)记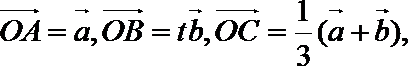
(2)若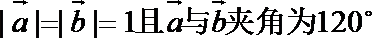
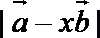
正确答案
解:(1)A、B、C三点共线知存在实数
即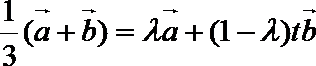
则
(2)
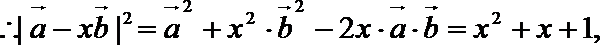
当
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析