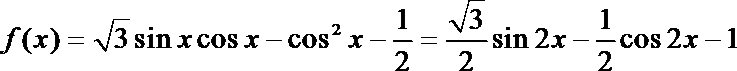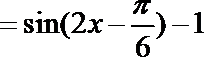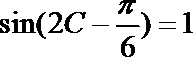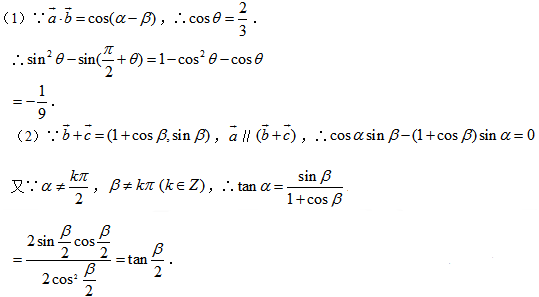- 平面向量
- 共1314题
12.已知向量a=(4,2),b=(x,3),且a∥b,则x的值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知点A分有向线段


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在△ABC中,角A,B,C的对边分别为a,b,c.设向量

(1)若

(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知

(1)求函数
(2)若在锐角



正确答案
(1) 

(2) 由(1)及

∵ 
∴ A=60°.
由余弦定理得3=b2+c2-2bccos60°,即(b+c)2=3+bc,
∴ (b+c)2=3+bc≤3+
所以,△ABC周长最大值为
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数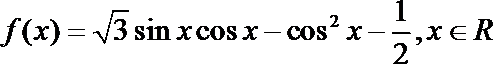
(1) 求函数
(2)已知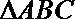
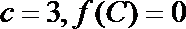
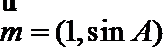
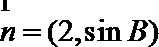
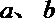
正确答案
(1)
∴ 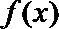
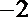


(2)∵ 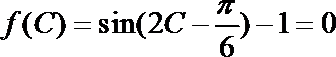
∵ 
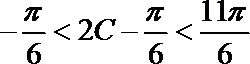

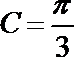
∵ 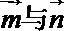
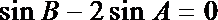
由正弦定理 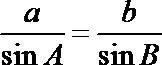
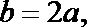
∵ 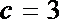
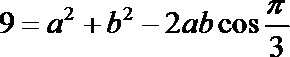
解方程组①②,得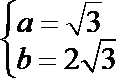
解析
解析已在路上飞奔,马上就到!
知识点
12.已知向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知向量a=(2,1),b=(-1,k),a·(2a-b)=0,则k=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.平面坐标系中,0为坐标原点,点A(3,1),点B(-1,3),若点C满足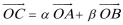
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设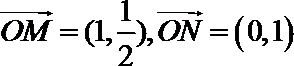
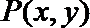
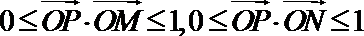
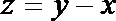
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在






(1)若

(2)若


正确答案
(1)
(2)

解析
解析已在路上飞奔,马上就到!
知识点
9.已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知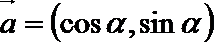

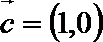
(1)若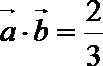
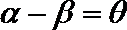

(2)若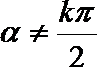

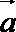
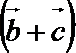
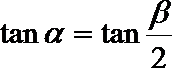
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.对于平面向量D={a|a=(x,y),x∈R,y∈R},我们作如下规定:对于任意两个向量a1=(x1,y1),a2=(x2,y2),当且仅当“x1>x2”或“x1=x2且y1>y2”,则“a1≫a2”按上述定义的关系“≫”,给出如下四个命题:
①若a1=(-1,2),a2=(1,-1),0=(0,0),则a1≫0≫a2;
②若a1≫a2,a2≫a3,则a1≫a3;
③若a1≫a2,a3≫a4,则对于任意a1+a3≫a2+a4.
其中真命题的序号为________.
正确答案
②③
解析
对于①,若a1=(-1,2),a2=(1,-1),0=(0,0),根据“≫”定义知a2≫0≫a1成立,所以a1≫0≫a2不正确;
对于②,设a1=(x1,y1),a2=(x2,y2),a3=(x3,y3),若a1≫a2,a2≫a3,
则

或
得x1>x3或x1=x3且y1>y3,即a1≫a3成立;
对于③,设a1=(x1,y1),a2=(x2,y2),a3=(x3,y3),a4=(x4,y4)若a1≫a2,则x1>x2或x1=x2且y1>y2,若a3≫a4,则x3>x4或x3=x4且y3>y4,则x1+x3>x2+x4或x1+x3=x2+x4且y1+y3>y2+y4,即a1+a3≫a2+a4成立,故②③为真命题
知识点
2.已知向量
正确答案
解析
由向量


考查方向
本题主要考查了平面向量的平行关系。
解题思路
本题考查平面向量的平行关系,解题步骤如下:利用平行的坐标公式求解。
易错点
本题必须注意坐标表示。
知识点
11.有一列向量






正确答案

解析
由题可知,差向量为(1,1),则向量an=(-21+n,12+n)。所以|an|2=(-21+n)2+(12+n)2=2n2-18n+585,则当n=4或5时取到最小值。
考查方向
本题主要考查了向量的模及新定义。
解题思路
本题考查向量的模,按照定义求解。
易错点
本题要注意按照定义求解。
知识点
扫码查看完整答案与解析