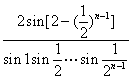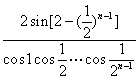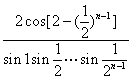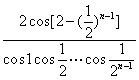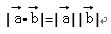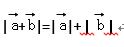- 平面向量
- 共1314题
4.已知

正确答案
解析
由题意,得


考查方向
解题思路
1)由题意得到

2)利用平面向量的的模长公式进行求解.
易错点
本题易在求
知识点
2.已知向量a=(2,x).b=(一4,2).若(a十b)∥(2a-b),则实数x的值为( )
正确答案
解析
本题属于平面向量中的基本问题,题目的难度是简单。
考查方向
本题主要考查了平面向量的平行的坐标表示,在近几年的各省高考题出现的频率较高。
解题思路
无
易错点
本题易在应用平行的坐标表示公式时发生错误。
知识点
已知向量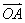
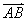
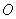

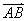
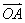
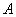
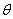

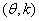
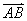
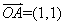
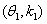
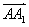
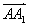
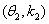
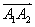
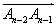

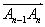
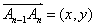
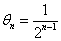
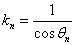
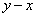
正确答案
解析
略
知识点
在边长为
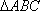
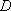
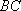
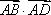
正确答案
解析
略
知识点
在直角梯形








中点,则
正确答案
解析
略
知识点
对于任意向量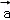
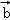
正确答案
解析
∵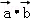
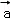
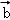
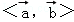
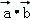
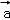
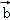
根据向量加法的平行四边形法则,|
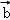
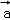
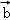
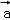
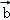
∵(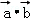
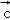
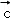

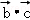
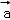
∵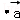
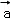

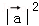
故选D
知识点
2.已知向量a=(2,x).b=(一4,2).若(a十b)∥(2a-b),则实数x的值为( )
正确答案
解析
试题分析:本题属于平面向量中的基本问题,题目的难度是简单。
考查方向
本题主要考查了平面向量的平行的坐标表示,在近几年的各省高考题出现的频率较高。
解题思路
本题考查平面向量的位置关系,解题步骤如下:
(1)由题可知,易得a+b=(-2,x+2),2a-b=(8,2x-2)。
(2)令8(x+2)=-2(2x-2),解得x= -1.
易错点
本题易在应用平行的坐标表示公式时发生错误。
知识点
17.已知数列{an}的前n项和为Sn ,向量a= (S n ,1),b= (2n — 1, 


①求数列{bn}的通项公式,
②设Cn =
正确答案
(1)
(2)①
解析
(1)∵






(2)①∵








考查方向
数列的通项公式和求和
解题思路
(1)利用
(2)①利用

易错点
1、利用定义求通项公式
2、第二问中错位相减法计算的准确性;
知识点
6.已知向量



正确答案
-3
解析
解析已在路上飞奔,马上就到!
知识点
14.设向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 在


正确答案
1
解析
∵△ABC中,∠A=90°
即
解得AB的边长为1,所以答案为1
考查方向
向量在几何中的应用
解题思路
根据直角三角形中三角函数的定义,结合题意得到边AB的长
易错点
对向量的运算性质掌握不好,计算出错
知识点
设向量


正确答案
解析
选A.如图,构造

所以A、B、C、D四点共圆,分析可知当线段AC为直径时,
知识点
如图,在矩形







正确答案
解析
由


∵



记


又∵

∴

本题也可建立以
知识点
已知向量




正确答案
解析
略
知识点
已知向量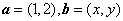

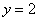
是“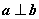
正确答案
解析
略
知识点
扫码查看完整答案与解析