- 平面向量
- 共1314题
13.设向量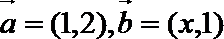
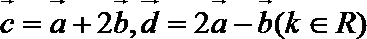
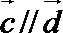
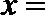
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18 .已知函数
(1)求函数
(2)已知






正确答案
(1)原式整理得
对称中心为
单调减区间为
(2)∵

∴C=
∵

及由正弦定理得
由余弦定理得
∴
解析
解析已在路上飞奔,马上就到!
知识点
21.已知向量a、b、c是同一平面内的三个向量,其中a=(1,2)
(1)若|c|=2
(2)若|b|=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知向量


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
9.已知向量a=(2,3),b=(-1,2),若ma+b与a-2b平行,则实数m等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量a=(sinx,-1),b=(cosx,
(1)当a∥b时,求cos2x-3sin2x的值;
(2)求f(x)=(a+b)·b的最小正周期和单调递增区间.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在△ABC中,角A、B、C所对的边分别为a、b、c, q=(



(1)求sin A的值;
(2)求三角函数式
正确答案
解:(1)∵

根据正弦定理,得
又



又
(2)原式

∵

∴
∴
∴

解析
解析已在路上飞奔,马上就到!
知识点
4.已知向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
设向量


正确答案
解析
选A.如图,构造

所以A、B、C、D四点共圆,分析可知当线段AC为直径时,
知识点
如图,在矩形







正确答案
解析
由


∵



记


又∵

∴

本题也可建立以
知识点
13.设向量a=(m,1),b=(1,2),且|a+b|2=|a|2+|b|2,则m= .
正确答案
-2
知识点
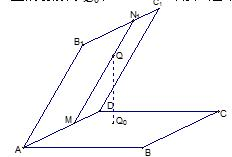
20.已知点O为




(Ⅰ)证明:
(Ⅱ)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
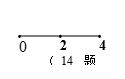
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间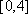
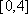

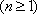
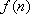
则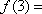
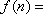
正确答案
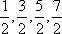
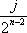
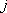
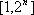
解析
略
知识点
已知向量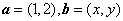

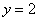
是“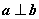
正确答案
解析
略
知识点
如图,在边长为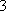
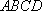
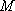
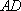
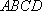
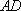
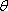
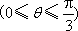
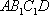
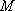
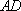
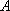
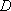
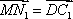
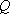
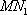
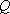
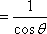
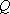
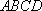
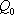

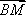
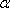
正确答案
解析
略
知识点
扫码查看完整答案与解析