- 直线、平面垂直的综合应用
- 共97题
已知向量m=(sinx,1)
(1)求A;
(2)将函数y=f(x)的图象像左平移


正确答案
(1)A=6
(2)函数g(x)在

解析
(1)
则
(Ⅱ)函数y=f(x)的图象像左平移

再将所得图象各点的横坐标缩短为原来的

当


故函数g(x)在

另解:由


则


于是
故


知识点
如图5,在棱长为



中点,点

(1)求证:
(2)在棱





此时
(3)求平面

正确答案
见解析。
解析
(1)
证明:连结

因为四边形

在正方体





因为



所以

因为


(2)
取



在平面



连结




因为

所以
故当




(3)
延长



则


过点



因为

所以

因为


所以


二面角的平面角,
因为
即
所以
在△


所以

即
因为
所以
所以
所以
故平面


(1)
证明:以点



分别为


则




所以

因为
所以
所以
(2)解:设


平面



所以
所以存在实数

因为

所以
所以

所以
故当




(3)解:由(1)知

设

则
即
取


所以

而

设平面


则

故平面


(3)
以点



分别为


则


则

设

则
取


所以

而

设平面


则

故平面


知识点
如图4,已知三棱柱ABC—A1B1C1的侧棱与底面垂直,且∠ACB=90°,
∠BAC=30°,BC=1,AA1=
的中点。
(1)求证:PN//平面ABC;
(2)求证:AB1⊥A1M;
(3)求二面角C1—A B1—A1的余弦值,
正确答案
见解析。
解析
(1)
证明:连结CB1,∵P是BC1的中点 ,∴CB1过点P,
∵N为AB1的中点,∴PN//AC,-
又∵



∴PN//平面ABC.
(2)证法一:
在直角ΔABC中,∵BC=1,∠BAC=30°,
∴ AC=A1C1=
∵棱柱ABC—A1B1C1的侧棱与底面垂直,且
原点,以C1B1所在的直线为x轴建立如图所示空间直角坐标系如图示,则




∴
∵
∴ A1M⊥AB1
【证法二:
连结AC1,在直角ΔABC中,∵BC=1,∠BAC=30°,
∴ AC=A1C1=
∵

∴

即AC1⊥A1M.
∵B1C1⊥C1A1,CC1⊥B1C1,且
∴B1C1⊥平面AA1CC1,
∴B1C1⊥A1M,又

【证法三:连结AC1,在直角ΔABC中,∵BC=1,∠BAC=30°,
∴ AC=A1C1=
∵
∴α+β=90° 即AC1⊥A1M.
∵B1C1⊥C1A1,CC1⊥B1C1,且
∴B1C1⊥平面AA1CC1,
∴B1C1⊥A1M,又
故A1M⊥面A B1C1,

(3)解法一:
∵棱柱ABC—A1B1C1的侧棱与底面垂直,且
以点C1为原点,以C1B1所在的直线为x轴建立如图所示空间直角坐标系,
依题意得





设面
由



同理可得面
故二面角的平面角
【解法二:
过C1作C1E⊥A1B1交A1B1于点E,过E作EF⊥AB1交AB1于F,连结C1 F,
∵平面AA1BB1⊥底面A1B1C1,∴ C1E⊥平面AA1BB1,
∴ C1E⊥AB1,∴ AB1⊥平面C1EF,∴ AB1⊥C1F,
故
在



又
知识点
不等式
正确答案
解析
略
知识点
已知函数f(x) = 
(1)求k的值;
(2)求f(x)的单调区间;
(3)设g(x)=(x2+x) 


正确答案
见解析。
解析
(1)由f(x) = 




(2)


当



于是


简证(3)
当


当

只需证
知识点
已知正方形ABCD的边长为1,点E是AB边上的动点,则

正确答案
1,1
解析
根据平面向量的数量积公式








知识点
如图,在直三棱柱






正确答案
60°
解析
方法一:如图1以








设平面A1BC1的一个法向量


则

设AD与平面A1BC1所成的角为
则
则
方法二:由题意知四边形AA1B1B是正方形,故AB1⊥BA1。
由AA1⊥平面A1B1C1得AA1⊥A1C1。
又A1C1⊥A1B1,所以A1C1⊥平面AA1B1B,故A1C1⊥AB1。
从而得 AB1⊥平面A1BC1。
设AB1与A1B相交于点O,则点O是线段AB1的中点。
连接AC1,由题意知△AB1C1是正三角形。
由AD,C1O是△AB1C1的中线知:AD与C1O的交点为重心G,连接OG。
知AB1⊥平面A1BC1,故OG是AD在平面A1BC1上的射影,
于是∠AGO是AD与平面A1BC1所成的角。
在直角△AOG中,AG=



所以sin∠AGO=

故∠AGO=60°,即AD与平面A1BC1所成的角为60°
知识点
若复数

正确答案
解析
略
知识点
若函数
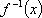
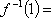
正确答案
1
解析
略
知识点
在平面直角坐标系








正确答案


解析
略
知识点
扫码查看完整答案与解析

























































