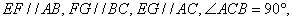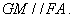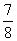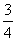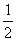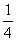- 直线、平面垂直的综合应用
- 共97题
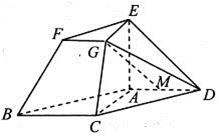
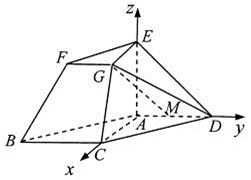
如图,在梯形










(1)求证:

(2)当


(3)求二面角
正确答案
见解析
解析
(1)在梯形


边形







(2)




为原点,












使












(3)过



由


即









知识点
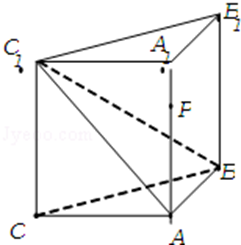
如图,侧棱垂直底面的三棱柱ABC﹣A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0)。
(1)当AA1=AB=AC时,求证:A1C⊥平面ABC1;
(2)若二面角A﹣BC1﹣C的平面角的余弦值为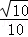
正确答案
见解析。
解析
(1)证明:∵AA1⊥面ABC,∴AA1⊥AC,AA1⊥AB。
又∵AB⊥AC,∴分别以AB,AC,AA1所在直线为x,y,z轴建立空间直角坐标系,则A(0,0,0),C1(0,1,1),B(1,0,0),C(0,1,0),A1(0,0,1),
∴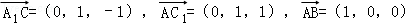
∴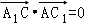
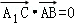
∴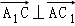
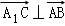
又∵AC1∩AB=A
∴A1C⊥平面ABC1。
(2)解:
分别以AB,AC,AA1所在直线为x,y,z轴建立空间直角坐标系。
则A(0,0,0),C1(0,t,3﹣2t),B(t,0,0),C(0,t,0),A1(0,0,3﹣2t),
∴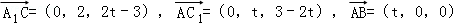
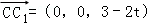
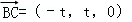
设平面ABC1的法向量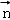
则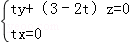
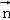
同理可求平面BCC1的法向量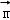
设二面角A﹣BC1﹣C的平面角为θ,
则有|cosθ|=|
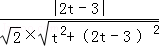
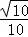
化简得5t2﹣16t+12=0,解得t=2(舍去)或t=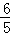
所以当t=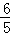
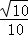
知识点
如图,设













(1)证明:

(2)证明:平面

正确答案
见解析
解析
(1)在折起后的图中,取




∵



∴

又∵



∴

∴四边形
∴
又∵



∴

(2) 在折起后的图中,∵

∴



∴
∵


又∵



∵

∵




∵

∵


∵



知识点
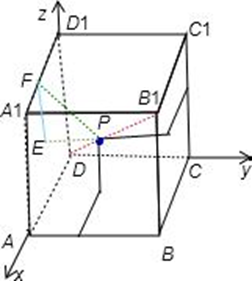
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点。
(1)求证:DA1⊥ED1 ;
(2)若直线DA1与平面CED1成角为45o,求
(3)写出点E到直线D1C距离的最大值及此时点E的位置(结论不要求证明)。
正确答案
见解析
解析
以D为坐标原点,建立如图所示的坐标系,则D(0,0,0),A(1,0,0),
B(1,1,0),C(0,1,0),D1(0,1,2),A1(1,0,1),设E(1,m,0)(0≤m≤1)
(1)证明:
所以DA1⊥ED1.-------------------------------------------------------------4分
(2)设平面CED1的一个法向量为


所以

因为直线DA1与平面CED1成角为45o,所以
所以


(3)点E到直线D1C距离的最大值为
知识点
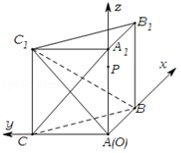
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2。
(1)若D为AA1中点,求证:平面B1CD⊥平面B1C1D;
(2)当AD的长等于多少时?二面角B1-DC-C1的大小为60°。
正确答案
见解析
解析
解析:(1)如图所示,以C为原点,CA、CB、CC1所在直线为x,y,z轴建立空间直角坐标系,
则C(0,0,0),A(1,0,0),B1(0,2,2),C1(0,0,2),D(1,0,1),
即
由
由
又DC1∩C1B1=C1,∴CD⊥平面B1C1D,平面B1CD⊥平面B1C1D,……6分
(2)设AD=a,则D点坐标为(1,0,a),
设平面B1CD的法向量为m=(x,y,z),则由
令z=-1,得m=(a,1,-1)。
又平面C1DC的法向量为n=(0,1,0),则由
即

知识点
在如图所示的几何体中,四边形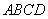
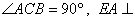
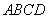
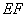
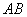
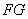
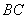
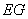
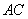
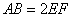
(1)若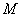
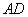

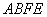
(2)若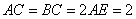
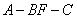
正确答案
见解析。
解析
(1)∵
∴
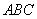
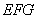
由于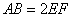
连接
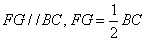
在平行四边形
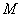
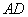
则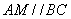
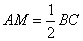
因此,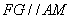
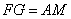
所以四边形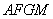
又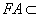

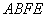
(2)解:∵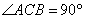
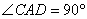
又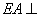

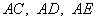
分别以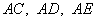
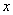
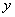
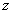
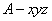
则
故
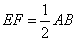
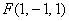
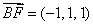
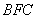
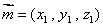
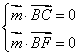
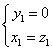
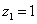

所以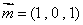
设平面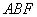
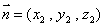
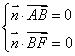
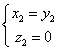
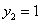
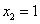
所以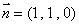
所以
故二面角
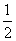
知识点
如图,圆柱的高为2,底面半径为3,AE、DF是圆柱的两条母线,B、C是下底面圆周
上的两点,已知四边形ABCD是正方形。
(1)求证:BC⊥BE;
(2)求正方形ABCD的边长;
(3)求直线AE与平面ABF所成角的正弦值。
正确答案
见解析。
解析
(1)∵AE是圆柱的母线∴AE⊥底而BEFC,
又
又∵ABCD是正方形,∴AB⊥BC
又AE⌒AB=A∴BC⊥面ABE
又
(2)∵四边形AEFD为矩形,且ABCD是正方形∴EF=BC,EF∥BC
∵BC⊥BE ∴四边形EFBC为矩形
∴BF为圆柱下底面的直径
设正方形ABCD的边长为x,则AB=EF=AB=x
在直角MEB中AE=2.AB=x,且
在直角ABEF中BF=6.EF=x,且
解得
(3)解法一:
过E作EH⊥BF于H,连结AH。
∵AE是圆柱的母线∴AE⊥底面BEFC,
又∵
∴AE⊥BF
∴BF⊥平面AEH
又
∴平面AEH⊥平面ABF
∴AH就是AE在平面ABF上的射影
∴∠EAH就是直线AE与平面ABF所成角
在Rt△BEF中,
在Rt△AEH中,
所以直线EF与平面ABF所成角的正弦值为
解法二:
如图以F为原点建立空间直角坐标系,
则A(


设面ABF的法向量为

即
,设直线AE与平面ABF所成角的大小为θ,则
所以直线EF与平面ABF所成角的正弦值为
解法三:如图以E为原点建立空间直角坐标系,
则 A (O,0, 2) ,B (4, 0, 0) ,F (O,
设面ABF的法向量为
令y=1.则
设直线EA与平面ABF所成角的大小为θ,则
所以直线EF与平面ABF所成角的正弦值为
知识点
与正方体ABCD﹣A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点( )
正确答案
解析
知识点
在区间[-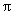
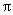
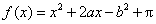
正确答案
解析
略
知识点
在棱长为4的正方体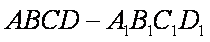
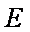
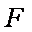
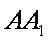
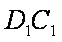
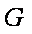

正确答案
12
解析
考察在面CDD1C1上的投影,点A的投影为D,点G的投影为棱CC1的中点,当点E运动到A1时,其投影为D1,当点F运动到C1时投影仍为C1,此时该投影构成的图形面积最大。
知识点
扫码查看完整答案与解析