- 直线、平面垂直的综合应用
- 共97题
1
题型:填空题
|
不等式
正确答案
解析
略
知识点
直线、平面垂直的综合应用
1
题型:填空题
|
已知正方形ABCD的边长为1,点E是AB边上的动点,则

正确答案
1,1
解析
根据平面向量的数量积公式








知识点
直线、平面垂直的综合应用
1
题型:简答题
|
如图,在直三棱柱






正确答案
60°
解析
方法一:如图1以








设平面A1BC1的一个法向量


则

设AD与平面A1BC1所成的角为
则
则
方法二:由题意知四边形AA1B1B是正方形,故AB1⊥BA1。
由AA1⊥平面A1B1C1得AA1⊥A1C1。
又A1C1⊥A1B1,所以A1C1⊥平面AA1B1B,故A1C1⊥AB1。
从而得 AB1⊥平面A1BC1。
设AB1与A1B相交于点O,则点O是线段AB1的中点。
连接AC1,由题意知△AB1C1是正三角形。
由AD,C1O是△AB1C1的中线知:AD与C1O的交点为重心G,连接OG。
知AB1⊥平面A1BC1,故OG是AD在平面A1BC1上的射影,
于是∠AGO是AD与平面A1BC1所成的角。
在直角△AOG中,AG=



所以sin∠AGO=

故∠AGO=60°,即AD与平面A1BC1所成的角为60°
知识点
直线、平面垂直的综合应用
1
题型:填空题
|
若函数
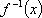
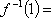
正确答案
1
解析
略
知识点
直线、平面垂直的综合应用
1
题型:填空题
|
在平面直角坐标系








正确答案


解析
略
知识点
直线、平面垂直的综合应用
下一知识点 : 线面角和二面角的求法
扫码查看完整答案与解析









