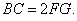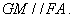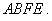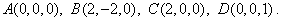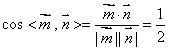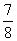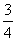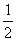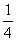- 直线、平面垂直的综合应用
- 共97题
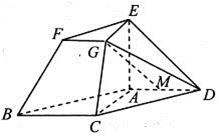
如图,在梯形










(1)求证:

(2)当


(3)求二面角
正确答案
见解析
解析
(1)在梯形


边形







(2)




为原点,












使












(3)过



由


即









知识点
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点。
(1)求证:DA1⊥ED1 ;
(2)若直线DA1与平面CED1成角为45o,求
(3)写出点E到直线D1C距离的最大值及此时点E的位置(结论不要求证明)。
正确答案
见解析
解析
以D为坐标原点,建立如图所示的坐标系,则D(0,0,0),A(1,0,0),
B(1,1,0),C(0,1,0),D1(0,1,2),A1(1,0,1),设E(1,m,0)(0≤m≤1)
(1)证明:
所以DA1⊥ED1.-------------------------------------------------------------4分
(2)设平面CED1的一个法向量为


所以

因为直线DA1与平面CED1成角为45o,所以
所以


(3)点E到直线D1C距离的最大值为
知识点
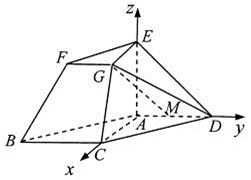
在如图所示的几何体中,四边形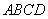
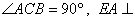
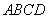
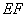
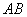
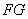
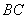
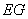
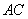
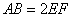
(1)若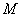
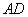

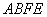
(2)若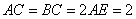
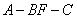
正确答案
见解析。
解析
(1)∵
∴
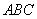
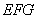
由于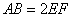
连接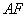
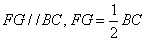
在平行四边形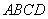
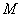
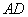
则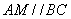
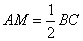
因此,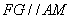
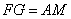
所以四边形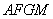
又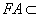

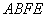
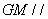
(2)解:∵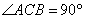
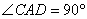
又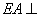

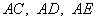
分别以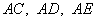
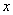
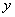
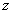
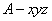
则
故
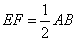
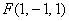
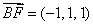
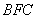
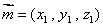
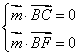
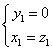
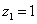

所以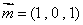
设平面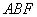
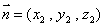
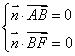
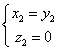
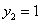
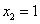
所以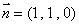
所以
故二面角
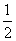
知识点
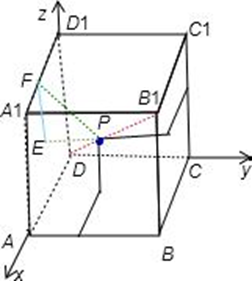
与正方体ABCD﹣A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点( )
正确答案
解析
知识点
在区间[-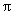
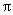
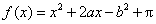
正确答案
解析
略
知识点
扫码查看完整答案与解析