直线、平面垂直的综合应用
共97题

· 直线、平面垂直的综合应用

直线、平面垂直的综合应用
共97题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

18．在直三棱柱ABC -A1B1C1中，已知AB=5，AC=4，BC=3，AA1=4，点D在棱AB上．

（Ⅰ）若D是AB中点，求证：AC1∥平面B1CD；

（Ⅱ）当时，求二面角的余弦值．

正确答案

(Ⅰ)

证明：连结BC1，交B1C于E，连接DE．

因为直三棱柱ABC-A1B1C1，D是AB中点，

所以侧面B B1C1C为矩形，DE为△ABC1的中位线，所以 DE// AC1．

因为 DE平面B1CD， AC1平面B1CD，所以 AC1∥平面B1CD．

（Ⅱ）

由（Ⅰ）知AC⊥BC，如图，以C为原点建立空间直角坐标系C-xyz．

则B (3, 0, 0)，A (0, 4, 0)，A1 (0, 4, 4)，B1 (3, 0, 4)．设D (a, b, 0)（，），

因为点D在线段AB上，且，即．

所以，，，, ,．

平面BCD的法向量为．设平面B1 CD的法向量为，

由，，得，

所以，，.所以．

所以二面角的余弦值为．

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质直线、平面垂直的综合应用

题型：简答题

简答题 · 12 分

18．如图，PA垂直于矩形ABCD所在的平面，AD=PA=2，，E、F分别是AB、PD的中点.

（Ⅰ）求证：平面PCE 平面PCD；

（Ⅱ）求四面体PEFC的体积．

正确答案

解:

（Ⅰ）

（Ⅱ）由（2）知，

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积平面与平面垂直的判定与性质直线、平面垂直的综合应用

题型：简答题

简答题 · 12 分

如图，已知梯形中,,分别是上的点，，是的中点，沿将梯形翻折，是平面平面。

（1）求证：BD⊥EG

（2）求二面角D-BF-C的余弦值

正确答案

见解析。

解析

（1），∴以点E为原点，分别以EB,EF,EA所在直线为X、Y、Z轴建立空间直角坐标系E—XYZ。

∵AB=BC=2AD=4，AE=,,G是BC的中点

∴B(2,0,0), D(0,2,2), E(0,0,0),G (2,2,0),

∴

（2）①

∴

②当最大值时，

∴B(2,0,0), D(0,2,2), F(0,3,0)

∴

设面BDF的法向量为，

则

令x=3，则y=2,z=1,,

又，

，

由的方向可得二面角D-BF-C的余弦值为。

知识点

直线、平面垂直的综合应用

题型：简答题

简答题 · 12 分

16．已知函数(R )．

（Ⅰ）求函数的最小正周期及单调递增区间；

（Ⅱ）内角的对边长分别为，若且试判断的形状，并说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

题型：简答题

简答题 · 14 分

20．已知是定义在上的增函数，且记。

（1）设，若数列满足，试写出的通项公式及前的和：

（2）对于任意．，若，判断的值的符号。

正确答案

（1），则，，即数列是以为首项，为公比的等比数列，

∴，；

（2）若，则，∵是定义在上的增函数

∴，则

∴，即，与矛盾，

∴

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

题型：单选题

单选题 · 5 分

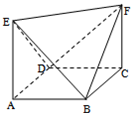
8．如图所示的几何体ABCDEF中，ABCD是平行四边形且AE∥CF，六个顶点任意两点连线能组成异面直线的对数是（）

A36

B28

C39

D20

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

题型：简答题

简答题 · 12 分

17. 在三棱锥中，是的中点，，其余棱长均为2.

（1）求证：平面平面；

（2）求二面角的平面角的正切值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

题型：简答题

简答题 · 12 分

19．已知f（x）=x3+ax2+bx+c,在x＝1与x＝－2时，都取得极值。

（1）求a，b的值；

（2）若x[－3，2]都有f（x）>恒成立，求c的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

题型：简答题

简答题 · 12 分

19.四棱锥底面是平行四边形，面面,,,分别为的中点.

（1）求证：

（2）求二面角的余弦值

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

题型：简答题

简答题 · 13 分

18.如图，在四面体ABCD中，O、E分别是BD、BC的中点，

（1）求证：平面BCD；

（2）求异面直线AB与CD所成角的余弦值；

（3）求点E到平面ACD的距离。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线、平面垂直的综合应用

继续学习学习下一知识点

下一知识点 : 线面角和二面角的求法

百度题库 > 高考 > 理科数学 > 直线、平面垂直的综合应用

扫码查看完整答案与解析