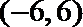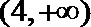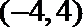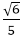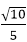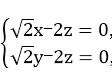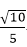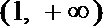- 直线、平面垂直的综合应用
- 共97题
4.已知一组数据4.7,4.8,5.1,5.4,5.5,则该组数据的方差是______________.
正确答案
0.1
知识点
9.正方形AP1P2P3的边长为4,点B,C分别是边P1P2,P2P3的中点,沿AB,BC,CA折成一个三棱锥P-ABC(使P1,P2,P3重合于P),则三棱锥P-ABC的外接球表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
(1)求证:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求点B到平面MAC的距离.
正确答案
方法1:(1)证明:∵PC⊥BC,PC⊥AB,∴PC⊥平面ABC,∴PC⊥AC.
(2)取BC的中点N,连MN.∵PM=∥CN,∴MN=∥PC,∴MN⊥平面ABC.
作NH⊥AC,交AC的延长线于H,连接MH.
由三垂线定理得AC⊥MH,∴∠MHN为二面角M﹣AC﹣B的平面角.
∵直线AM与直线PC所成的角为60°,
∴在Rt△AMN中,∠AMN=60°.
在△ACN中,
在Rt△AMN中,
在Rt△NCH中,
在Rt△MNH中,∵

故二面角M﹣AC﹣B的余弦值为
(3)作NE⊥MH于E.∵AC⊥平面MNH,∴AC⊥NE,∴NE⊥平面MAC,
∴点N到平面MAC的距离为
∵点N是线段BC的中点,
∴点B到平面MAC的距离是点N到平面MAC的距离的两倍为
方法2:(1)证明:∵PC⊥BC,PC⊥AB,∴PC⊥平面ABC,∴PC⊥AC.
(2)在平面ABC内,过C作BC的垂线,并建立空间直角坐标系如图所示.
设P(0,0,z),则

∵
且z>0,∴

设平面MAC的一个法向量为
得


平面ABC的一个法向量为

显然,二面角M﹣AC﹣B为锐二面角,∴二面角M﹣AC﹣B的余弦值为
(3)点B到平面MAC的距离
解析
解析已在路上飞奔,马上就到!
知识点
21.已知二次函数


(1) 求f (x) 的定义域D和值域 A;
(2)试用函数单调性的定义解决下列问题:
若存在实数




(3)是否存在实数t,使得A B成立?若存在,求实数t 的取值范围;若不存在,请说明理由.
正确答案
(1)定义域D =[-1,1] 值域 A=
(2)在


则
得
得
同理 由在

所以 
由
(3)由(2)的单调性分析同理可得 t 的不同取值,函数g(x)的单调性
① 当 t≤0时,函数 g(x) = x 3-3tx + 在 x∈[0,1]单调递增,∴B = [,
∴
② 当 0 < t < 1 时,函数 g(x)的减区间为:
g(x)在 x = 达到最小值。

③ 当t≥1时,函数 g(x) 在区间 [0,1]单调递减,
∴B = [
∴
综上所述:t的取值范围是:
解析
解析已在路上飞奔,马上就到!
知识点
10.已知实数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数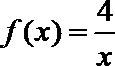
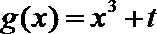
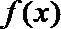
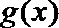
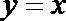
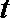
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
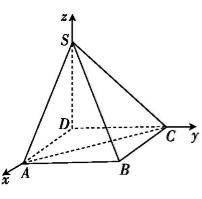
9.如图,四棱锥S-ABCD的底面是正方形,SD
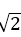
正确答案
解析
如图,以D为原点建立空间直角坐标系Dxyz.
则D(0,0,0),A(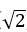

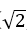
得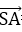
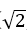
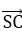
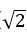
设平面ACS的一个法向量为n=(x,y,z),
则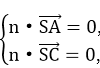
取z=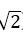
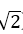
易知平面ASD的一个法向量为 =(0,
设二面角C-AS-D的大小为θ,则cos θ=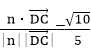
即二面角C-AS-D的余弦值为
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
(2011•福建)在矩形ABCD中,点P在AD上,AB=2,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB,BC于点E,F,连接EF(如图①).
(1)当点E与点B重合时,点F恰好与点C重合(如图②),求PC的长;
(2)探究:将直尺从图②中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,请你观察、猜想,并解答:
①tan∠PEF的值是否发生变化?请说明理由;
②直接写出从开始到停止,线段EF的中点经过的路线长.
正确答案
(1)PC=2

解析
(1)由勾股定理求PB,利用互余关系证明△APB∽△DCP,利用相似比求PC;
(2)tan∠PEF的值不变.过F作FG⊥AD,垂足为G,同(1)的方法证明△APB∽△DCP,得相似比


(3)如图3,画出起始位置和终点位置时,线段EF的中点O1,O2,连接O1O2,线段O1O2即为线段EF的中点经过的路线长,也就是△BPC的中位线.
(1)在矩形ABCD中,∠A=∠D=90°,
AP=1,CD=AB=2,则PB=
∴∠ABP+∠APB=90°,
又∵∠BPC=90°,
∴∠APB+∠DPC=90°,
∴∠ABP=∠DPC,
∴△APB∽△DCP,
∴



∴PC=2
(2)tan∠PEF的值不变.
理由:过F作FG⊥AD,垂足为G,
则四边形ABFG是矩形,
∴∠A=∠PFG=90°,GF=AB=2,
∴∠AEP+∠APE=90°,
又∵∠EPF=90°,
∴∠APE+∠GPF=90°,
∴∠AEP=∠GPF,
∴△APE∽△GPF,
∴


∴Rt△EPF中,tan∠PEF=
∴tan∠PEF的值不变;
(3)线段EF的中点经过的路线长为
本题考查了相似三角形的判定与性质,矩形的性质,解直角三角形.关键是利用互余关系证明相似三角形.
知识点
19.如图,在四面体PABC中,PA=PB,CA=CB,D、E、F、G分别是PA,AC、CB、BP的中点.
(1)求证:D、E、F、G四点共面;
(2)求证:PC⊥AB;
(3)若△ABC和△PAB都是等腰直角三角形,且AB=2,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析