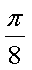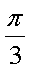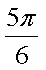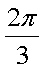- 函数的定义域及其求法
- 共125题
已知定义在




正确答案
解析
由题

故


记

且
故方程
知识点
已知函数 
(1)求函数
(2)设




(3)对(2)中





正确答案
(1)
(3)
解析
解析:

又


(2)因为
令

∴


由题意知g(a)即为函数
注意到直线

因为a<0时,函数y=m(t), 
①若


②若


③若


综上有

(3)易得
由

即要使



只需
求出m的取值范围是
知识点
将52名志愿者分成A,B两组参加义务植树活动,A组种植150捆白杨树苗,B组种植200捆
沙棘树苗,假定A,B两组同时开始种植。
(1)根据历年统计,每名志愿者种植一捆白杨树苗用时

(2)在按(1)分配的人数种植1小时后发现,每名志愿者种植一捆白杨树苗用时仍为

续种植,求植树活动所持续的时间.
正确答案
见解析
解析
解:(1)设A组人数为


则A组活动所需时间
B组活动所需时间
令


所以两组同时开始的植树活动所需时间
而

所以当A、B两组人数分别为
(2)A组所需时间为1+
B组所需时间为
所以植树活动所持续的时间为
知识点
对于定义在区间D上的函数f(x),若任给x0∈D,均有f(x0)∈D,则称函数f(x)在区间D上封闭。
(1)试判断f(x)=x﹣1在区间[﹣2.1]上是否封闭,并说明理由;
(2)若函数g(x)=
(3)若函数h(x)=x3﹣3x在区间[a,b[(a,b∈Z)上封闭,求a,b的值。
正确答案
见解析
解析
(1)f(x)=x﹣1在区间[﹣2,1]上单调递增,所以f(x)的值域为[﹣3,0]
而[﹣3,0]⊈[﹣2,1],所以f(x)在区间[﹣2,1]上不是封闭的;
(2)因为g(x)=

①当a=3时,函数g(x)的值域为{3}⊆[3,10],适合题意。
②当a>3时,函数g(x)=3+

由

③当a<3时,在区间[3,10]上有
综上所述,实数a的取值范围是3≤a≤31;
(3)因为h(x)=x3﹣3x,所以h′(x)=3x2﹣3=3(x+1)(x﹣1),
当x∈(﹣∞,﹣1)时,h′(x)>0,当x∈(﹣1,1)时,h′(x)0。
所以h(x)在(﹣∞,﹣1)上单调递增,在(﹣1,1)上递减,在(1,+∞)上递增。
①当a<b≤﹣1时,h(x)在区间[a,b]上递增,所以
即
②当a≤﹣1且﹣1<b≤1时,因h(x)max=h(﹣1)=2>b,矛盾,不合题意
③当a≤﹣1且b>1时,因为h(﹣1)=2,h(1)=﹣2都在函数的值域内,故a≤﹣2,b≥2,
又

④当﹣1≤a<b≤1时,h(x)在区间[a,b]上递减,
而a,b∈Z,经检验,满足﹣1≤a<b≤1的整数组a,b均不合式。
⑤当﹣1<a<1且b≥1时,因h(x)min=h(1)=﹣2<a,矛盾,不合题意。
⑥当b>a≥1时,h(x)在区间[a,b]上递增,所以
即
综上所述,所求整数a,b的值为a=﹣2,b=2
知识点
已知f(x)是定义在[﹣1,1]上的奇函数,满足f(1)=1,且当a,b∈[﹣1,1],a+b≠0,有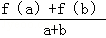
正确答案
解析
函数f(x)在[﹣1,1]上是增函数。
设﹣1≤x1<x2≤1,
∵f(x)是定义在[﹣1,1]上的奇函数,
∴f(x2)﹣f(x1)=f(x2)+f(﹣x1)。
又x1<x2,∴x2+(﹣x1)≠0,由题设有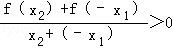
∵x2+(﹣x1)=x2﹣x1>0,
∴f(x2)+f(﹣x1)>0,
即f(x1)<f(x2),
∴函数f (x) 在[﹣1,1]上是增函数,
∴f(x)max=f(1)=1,
∴f(x)≤m2﹣2am+1对任意x∈[﹣1,1]恒成立,
只需1≤m2﹣2am+1对a∈[﹣1,1]恒成立,
即 m2﹣2am≥0对a∈[﹣1,1]恒成立
设g(a)=m2﹣2mp,则
有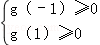
解得 m≤﹣2或m≥2,
∴m的取值范围是(﹣∞,﹣2]∪[2,+∞)。
知识点
患感冒与昼夜温差大小相关,居居小区诊所的某医生记录了四月份四个周一的温差情况与因患感冒到诊所看病的人数如下表:
用最小二乘法求出

参考公式:
正确答案
解析
由已知表中数据可求得
从而得
再由

知识点
将函数


正确答案
解析
由题易得





知识点
定义行列式运算: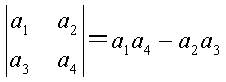
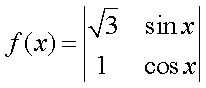
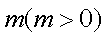
正确答案
解析
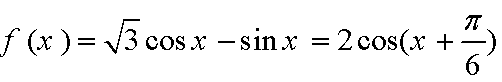
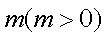
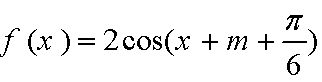
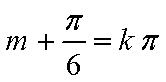
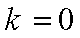
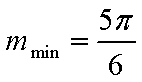
知识点
定义运算


正确答案
解析
由


知识点
设函数
(1)若对定义域内的任意


(2)若函数
(3)若


正确答案
见解析
解析
(1)由



因为对

故有
又

经检验,当




故满足
(2)



即

若



因为



综上所述,实数b的取值范围是
(3)当

则


所以函数




即






知识点
扫码查看完整答案与解析