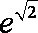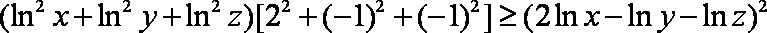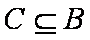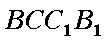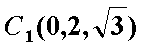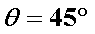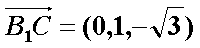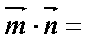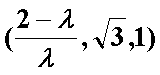- 函数的定义域及其求法
- 共125题
若复数


正确答案
解析
第一步识别条件:纯虚数。z=a+bi a=0且b不等于0
第二步转化条件:

第三步看问定向: 再看方向:则实数
知识点
若


正确答案
8
解析
略
知识点
已知
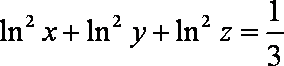
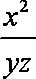
正确答案
解析
知识点
下图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是
正确答案
解析
略
知识点
设集合A为函数y =ln(-x2-2x+8)的定义域,集合B为函数
y=x+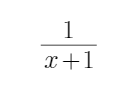
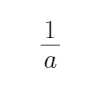
(1)求A∩B; (2)若
正确答案
见解析
解析
(1)由-x2-2x+8>0,解得A=(-4,2),又y=x+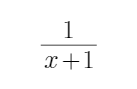
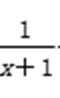
所以B=(-∞,-3]∪ [1,+∞),所以A∩B=(-4,-3]∪[1,2),
(2)因为∁RA=(-∞,-4]∪[2,+∞)。
由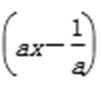
① 当a>0时,由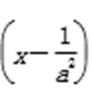

② 当a<0时,由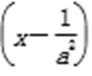
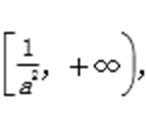
欲使C⊆∁RA,则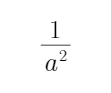
解得-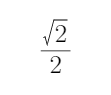
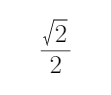
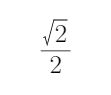
综上所述,所求a的取值范围是
知识点
已知函数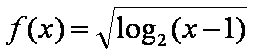
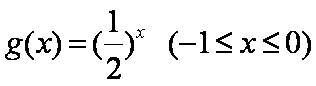
(1)求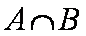
(2)若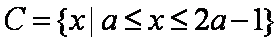
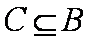
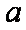
正确答案
见解析
解析
(1)由题意得: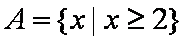
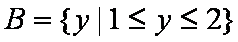
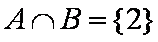
(2)由(1)知: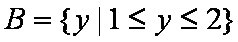
①当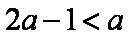
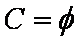
②当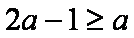
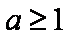
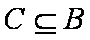

解得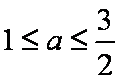
综上,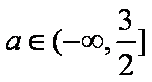
知识点
已知f(x)=|x+1|+|x-1| ,不等式f(x)
(1)求M;
(2)当a,b

正确答案
见解析。
解析
(1)由

当



当



当



综上,
(2)当


即:


∴

也就是
∴
即:
即
知识点
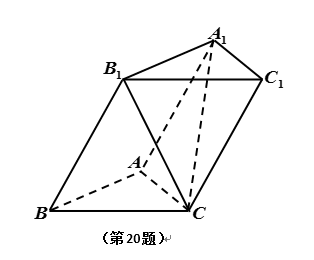
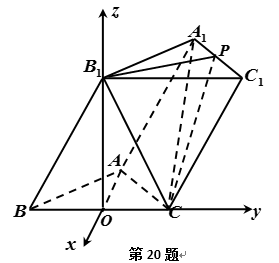
如图,三棱柱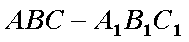
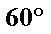
(1)求直线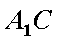
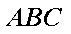
(2)在线段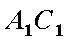
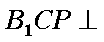
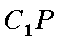
正确答案
见解析
解析
(1)过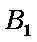
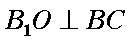
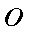
∵侧面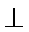
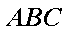
∴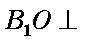
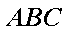
∴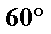
又∵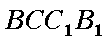
以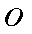
则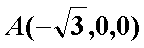
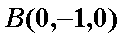
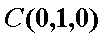
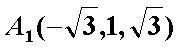
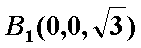
∴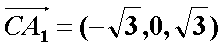
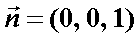
设直线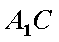
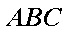
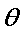
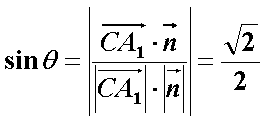
所以,直线
(2)假设在线段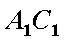
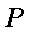
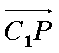
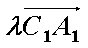
则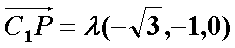
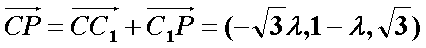
设平面
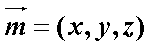
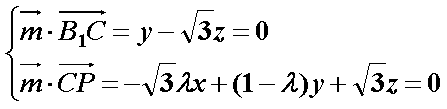
令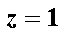
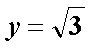
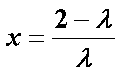
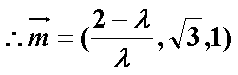
设平面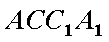
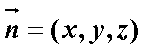
令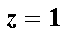
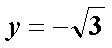
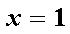
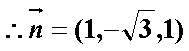
要使平面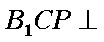
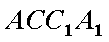
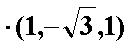
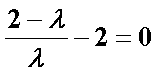
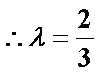
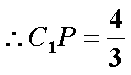
知识点
已知集合


正确答案
解析
因为集合


知识点
已知椭圆
(1)求椭圆的方程;
(2)若C、D分别是椭圆长轴的左、右端点,动点M满足

(3)在(2)的条件下,试问在x轴上是否存在异于点C的定点Q,使以线段MP为直径的圆恒过直线DP、MQ的交点,若存在,求出Q的坐标,若不存在,说明理由。
正确答案
见解析
解析
(1)如图,由题知

(2)C(-2,0),D(2,0),则可设

(3)设


知识点
扫码查看完整答案与解析