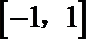- 函数的定义域及其求法
- 共125题
1
题型：
单选题
|
1．已知实数集R，集合
A
B
C
D
正确答案
B
解析
解析已在路上飞奔，马上就到！
知识点
交、并、补集的混合运算函数的定义域及其求法
1
题型：填空题
|
13．函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
函数的定义域及其求法
1
题型：简答题
|
21．某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的容积为
（1） 写出y关于r的函数表达式，并求该函数的定义域；
（2） 求该容器的建造费用最小时的r．
正确答案
（1）设容器的容积为V，
由题意知V＝πr2l＋
又V＝
∴ πr2l＋
∴ 0<r≤2．
所以建造费用
（2）由（1）得
0<r≤2． 由于c>3，所以c－2>0．
当r3－
∴ 当y' >0时，r>
当y' <0时，0<r<
∴ 函数y在（0， 
在[
① 当2≤
函数y在（0， 2]上为减函数，
所以r＝2是函数y的最小值点．
② 当2≥
∴ 函数y在（0， 
∴所以r＝
综上所述，当3<c≤
当c>
解析
解析已在路上飞奔，马上就到！
知识点
函数的定义域及其求法
1
题型：填空题
|
21．函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
函数的定义域及其求法
1
题型：
单选题
|
9. 如图，正方体
为
A点
B
C
D直线
正确答案
D
解析
解析已在路上飞奔，马上就到！
知识点
函数的定义域及其求法
下一知识点 : 函数的值域
扫码查看完整答案与解析