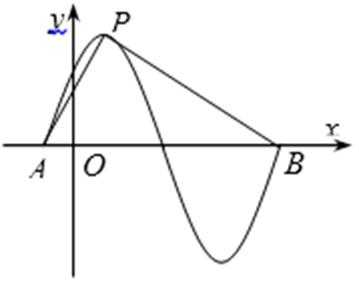
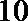- 正弦函数的图象
- 共33题
20.已知函数y=3sin
(1)用五点法在给定的坐标系中作出函数一个周期的图象;
(2)求此函数的振幅、周期和初相;
(3)求此函数图象的对称轴方程、对称中心。
正确答案
列表:
描点、连线,如图所示:
(2)周期T=



(3)令


得x=2k

令




对称中心为
解析
解析已在路上飞奔,马上就到!
知识点
6.函数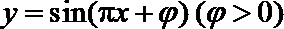
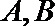
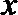
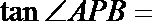
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若关于




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 设等比数列{an}的前n项和为Sn,则x=S2n+S22n, y=Sn(S2n+S3n)的大小关系是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数f(x)=|sin x|的图象与直线y=kx(k>0)有且仅有三个交点,交点的横坐标的最大值为α,令m=

正确答案
解析
作出函数f(x)=|sin x|的图象与直线y=kx(k>0)的图象,如图.
要是两个函数有且仅有三个交点,则由图象可知,直线在(π,
当x∈(π,
此时f'(x)=-cos x,则-cos α=-
所以m=



知识点
15.若不等式logax>sin 2x (a>0,a≠1)对任意x∈(0,
正确答案
(
解析
记y1=logax,y2=sin 2x,原不等式相当于y1>y2,作出两个函数的图象,如图所示,可知当y1=logax过点A(



知识点
12.已知


正确答案
17
解析
本题主要考查了函数的图像求交点。
考查方向
本题主要考查了函数的图像求交点。
解题思路
本题考查函数图像求交点,分别作出f(x),g(x)的图像求解。
易错点
本题要注意利用图像求解。
知识点
4.已知函数




正确答案
解析
由题意得













考查方向
本题主要考查三角函数的图像和性质、诱导公式等知识,意在考查考生对于三角函数基础知识的掌握程度。
解题思路
1.先根据题中条件求出函数
2.然后利用对称中心的坐标公式求出此函数的对称中心。
易错点
1.图像平移时容易错写成
2.混淆对称中心与对称轴导致结果出错。
知识点
10. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数



正确答案
解析





又因为




考查方向
解题思路
利用正弦曲线的对称性,知道





易错点
不会作出分段函数图像,找不到对称关系。
知识点
扫码查看完整答案与解析