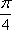- 与面积、体积有关的几何概型
- 共45题
设曲线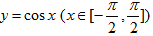
连结曲线与坐标轴的交点得到的封闭区域为N,向区域M内随机投
一点(该点落在区域M内任何一点是等可能的),则所投的点落在区
域N内的概率是________.
正确答案
解析


区域N的面积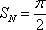
概率为
知识点
中国蓝球职业联赛(CBA)的总决赛采用七局四胜制,当两支实力水平相当的球队进入总决赛时,根据以往经验,第一场比赛中组织者可获票房收入

(1)组织者至少可以获得多少票房收入?
(2)决出胜负所需比赛场次的均值.
正确答案
见解析
解析
(1)设n为比赛的场数,
则



(2)(理)当







所以决出胜负的比赛场次的均值为6场. (12分)
知识点
意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数: 1,1,2,3,5,8,13,…其中从第三个数起,每一个数都等于他前而两个数的和,该数列是一个非常美丽、和谐的数列,有很多奇妙的属性,比如:随着数列项数的增加,前一项与后一项之比越逼近黄金分割0.6180339887…,人们称该数列{an}为“斐波那契数列”,若把该数列{an}的每一项除以4所得的余数按相对应的顺序组成新数列{bn},在数列{bn}中第2014项的值是________;数列{bn}中,第2014个值为1的项的序号是________.
正确答案
3,4027.
解析
经过计算,数列{bn}是周期为6的周期数列,前6项为:1,1,2,3,1,0,
∴第2014=6×335+4项的值是3;
∵每个周期内含有三个1,2014=3×671+1,
∴第2014个值为1的项的序号是6×671+1=4027.
知识点
甲、乙两位同学进行篮球三分球投篮比赛,甲每次投中的概率为

(1)记甲投中的次数为ξ,求ξ的分布列及数学期望Eξ;
(2)求乙至多投中2次的概率;
(3)求乙恰好比甲多投进2次的概率。
正确答案
见解析
解析
(1)

…………4分

(2)乙至多投中2次的概率为
(3)设乙比甲多投中2次为事件A,乙恰投中2次且甲恰投中0次为事件B1,
乙恰投中3次且甲恰投中1次为事件B2,
则

所以乙恰好比甲多投中2次的概率为
知识点
现有长分别为





(1)当




(2)当


②令


正确答案
见解析。
解析
(1)事件

(2)①


∴
……………………………………………………9分
②



知识点
扫码查看完整答案与解析