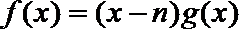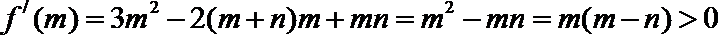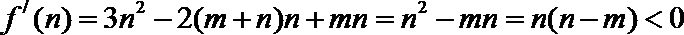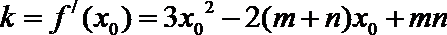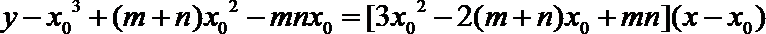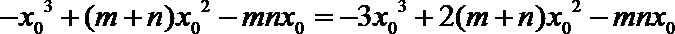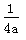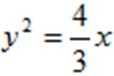- 抛物线及其性质
- 共507题
22. 抛物线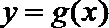
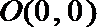
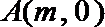
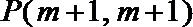
其中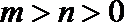
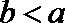
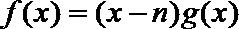

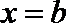
(1)用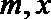
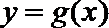
(2) 比较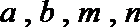
(3)若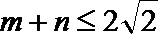
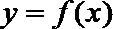
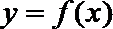
正确答案
(1)由抛物线经过点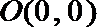
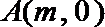
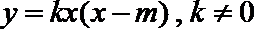
又抛物线过点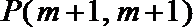
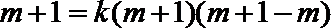
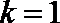
所以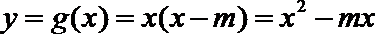
(2)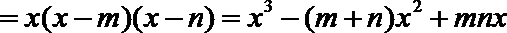
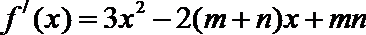
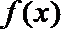

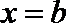
故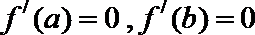
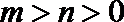
又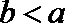
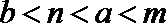
(3)设切点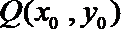
又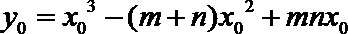
又切线过原点,故
所以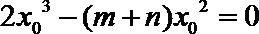
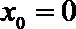
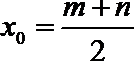
两条切线的斜率为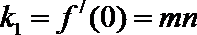
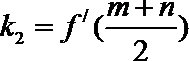
由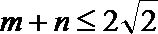
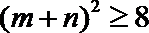
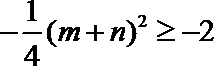
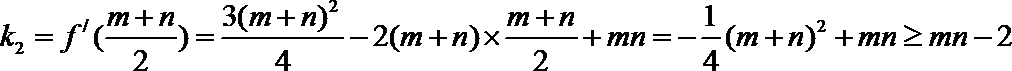
所以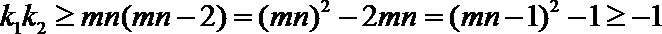
又两条切线垂直,故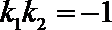
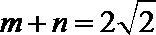
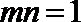
所以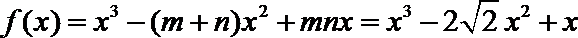
解析
解析已在路上飞奔,马上就到!
知识点
4.已知抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.抛物线y=ax2(a≠0)的准线方程为__________________.
正确答案
y=-
解析
解析已在路上飞奔,马上就到!
知识点
22.抛物线y=g(x)过点O(0,0)、A(m,0)与点P(m+1,m+1),其中m>n>0,b<a,设函数f(x)=(x﹣n)g(x)在x=a和x=b处取到极值.
(1)用m,x表示y=g(x)并比较a,b,m,n的大小(要求按从小到大排列);
(2)若
正确答案
(1)由抛物线经过点O(0,0)、A(m,0)
设抛物线方程y=kx(x﹣m)(k≠0),
又抛物线过点P(m+1,m+1),则m+1=k(m+1)(m+1﹣m),得k=1,
所以y=g(x)=x(x﹣m).
∴f(x)=(x﹣n)g(x)=x3﹣(m+n)x2+mnx,
∴f′(x)=3x2﹣2(m+n)x+mn,
∵函数f(x)在x=a和x=b处取到极值,
∴f′(a)=0,f′(b)=0,
∵m>n>0,
∴f′(m)=3m2﹣2(m+n)m+mn=m(m﹣n)>0
f′(n)=3n2﹣2(m+n)n+mn=n(n﹣m)<0,
又b<a,故b<n<a<m.
(2)设切点Q(x0,y0),则切线的斜率k=f′(x0)=3x02﹣2(m+n)x0+mn
又y0=



又切线过原点,故﹣

所以2


两条切线的斜率为k1=f′(0)=mn,
由

∴
所以
又两条切线垂直,故k1k2=﹣1,
所以上式等号成立,有
所以f(x)=x3﹣(m+n)x2+mnx=x3﹣
解析
解析已在路上飞奔,马上就到!
知识点
20.已知AB是抛物线
(Ⅰ)求证:直线AB恒过一定点,并求出该点坐标;
(Ⅱ)取抛物线上一点







正确答案
解:
(Ⅰ)由已知可得直线AB的斜率存在,设其方程为y=kx+b
联立抛物线方程得:
由

(Ⅱ)设圆心Q坐标为(0,q)
当




当



则过P的抛物线的切线方程为
则过P且与切线垂直的直线记为L:
坐标为(0,


圆Q半径取得最大值,圆心为(0,2)半径为
综上所求圆Q的标准方程是:
解析
解析已在路上飞奔,马上就到!
知识点
14.右图是抛物线形拱桥,当水面在
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.抛物线


正确答案
(0,1)
解析
解析已在路上飞奔,马上就到!
知识点
15.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.过点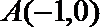
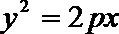
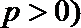
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知抛物线











(1)求⊙M和抛物线
(2)若


(3)过



正确答案
解:(1)因为


设⊙M的半径为


(2)设

所以当

(3)以点Q这圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦
设点

从而直线QS的方程为
因为
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析