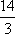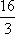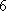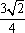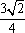- 抛物线及其性质
- 共507题
设函数f(x)=
正确答案
解析
当x>0时,f(x)=
f[f(x)]=


知识点
如图,在正方形














(1)求证:点

(2)过点







正确答案
(1)

解析
(1)依题意,过



设






(2)依题意:直线

由
此时


设:
又
分别带入
直线


知识点
若曲线



正确答案

解析




知识点
设a,b,c均为正数,且a+b+c=1,证明:
(1)ab+bc+ac≤
(2)
正确答案
见解析
解析
(1)由a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ca,
得a2+b2+c2≥ab+bc+ca.
由题设得(a+b+c)2=1,即a2+b2+c2+2ab+2bc+2ca=1.
所以3(ab+bc+ca)≤1,即ab+bc+ca≤
(2)因为


故
即
所以
知识点
设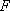
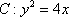

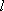
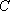
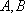
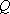
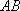
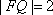
正确答案
解析
由已知得到: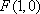
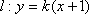
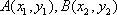
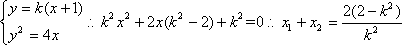
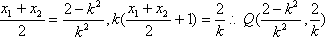
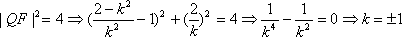
知识点
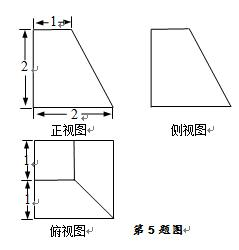
某四棱台的三视图如图1所示,则该四棱台的体积是 ( )
正确答案
解析
B;由三视图可知,该四棱台的上下底面边长分别为1和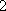
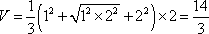
知识点
已知双曲线

正确答案
解析
设A点坐标为(x0,y0),则由题意,得S△AOB=|x0|·|y0|=








知识点
定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离,已知曲线C1:y=x 2+a到直线l:y=x的距离等于C2:x 2+(y+4) 2 =2到直线l:y=x的距离,
则实数a=______________。
正确答案
解析
C2:x 2+(y+4) 2 =2,圆心(0,—4),圆心到直线l:y=x的距离为:

另一方面:曲线C1:y=x 2+a,令




知识点
在△ABC中,a=3,
(1)求cos A的值;
(2)求c的值。
正确答案
(1) 
解析
(1)因为a=3,
所以在△ABC中,由正弦定理得
所以

(2)由(1)知,cos A=
所以sin A=
又因为∠B=2∠A,
所以cos B=2cos2A-1=
所以sin B=
在△ABC中,sin C=sin(A+B)=sin Acos B+cos Asin B=
所以c=
知识点
设抛物线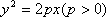
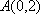
正确答案
解析
本题考查了中点坐标公式、抛物线的准线方程
由题意得B(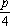

知识点
扫码查看完整答案与解析