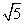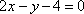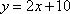- 抛物线及其性质
- 共507题
抛物线











正确答案
解析
略
知识点
若双曲线

正确答案
解析
略
知识点
已知抛物线









(1)求抛物线
(2)证明△ABO与△MNO的面积之比为定值.
正确答案
见解析
解析
(1)由焦点坐标为
所以
所以抛物线

(2)当直线



所以
当直线


设



解 

所以

综上
知识点
已知抛物线





正确答案
解析
∵直线l的方程分别为:
y =











所以Eξ=






知识点
已知点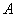
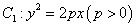
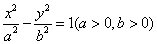
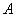
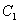
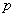
正确答案
解析
略
知识点
曲线









正确答案
解析
略
知识点
在平面直角坐标系xOy中,抛物线C的焦点在y轴上,且抛物线上的点P(x0,4)到焦点F的距离为5,斜率为2的直线l与抛物线C交于A,B两点。
(1)求抛物线C的标准方程,及抛物线在P点处的切线方程;
(2)若AB的垂直平分线分别交y轴和抛物线于M,N两点(M,N位于直线l两侧),当四边形AMBN为菱形时,求直线l的方程。
正确答案
(1)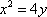
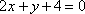
(2)
解析
(1)依题意设抛物线C: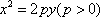
因为点P到焦点F的距离为5,
所以点P到准线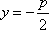
因为P(x0,4),所以由抛物线准线方程可得 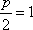
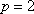
所以抛物线的标准方程为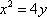
即 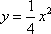
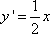
所以 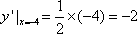
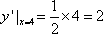
所以 点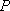
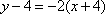
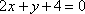
点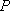
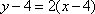
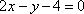
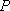
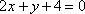
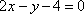
(2)设直线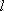
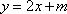
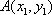
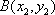
联立 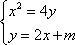
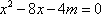
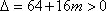
所以 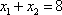
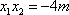
所以 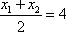
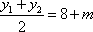
即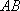
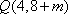
所以 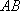
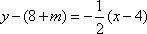
因为 四边形AMBN为菱形,
所以 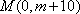
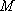
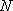
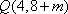
所以 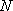
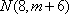
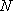
所以 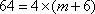
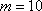
所
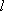
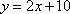
知识点
曲线



① 曲线

② 若点


③ 若点


其中,所有正确结论的序号是____________。
正确答案
①②③
解析
略
知识点
已知抛物线




(1)若

(2)设点





正确答案
(1)直线
(2)最小值是
解析
(1)解:依题意


将直线


设



因为
所以
联立①和②,消去

所以直线

(2)解:由点







所以四边形

因为

所以


知识点
在平面直角坐标系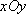
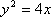
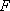
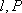
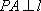
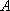
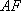
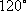
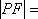
正确答案
4
解析
抛物线的焦点坐标为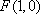
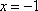
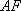
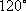
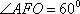
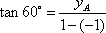
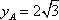

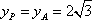
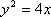
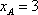
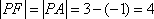
知识点
扫码查看完整答案与解析