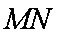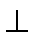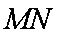- 抛物线及其性质
- 共507题
已知抛物线x2=4y上一点P到焦点F的距离是5,则点P的横坐标是 。
正确答案
±4
解析
根据抛物线的定义可知P到焦点的距离为5,则其到准线距离也为5。
又∵抛物线的准线为y=﹣1,
∴P点的纵坐标为5﹣1=4。
将y=4 代入抛物线方程得:4×4=x2,解得x=±4
故答案为:±4。
知识点
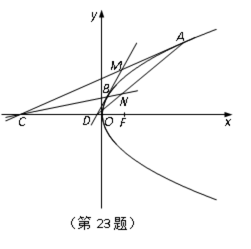
如图,在平面直角坐标系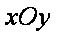
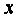
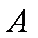
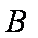
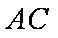
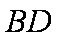
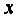
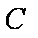
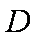
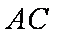
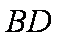
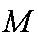
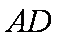
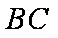
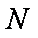
(1)求抛物线的标准方程;
(2)求证: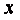
(3)若直线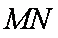
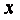
求证:直线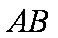
正确答案
见解析
解析
解:(1)设抛物线的标准方程为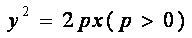
由题意,得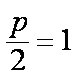
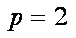
所以抛物线的标准方程为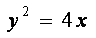
(2)设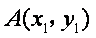
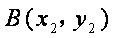
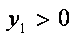
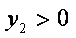
由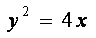
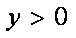
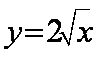
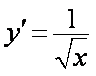
所以切线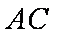
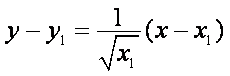
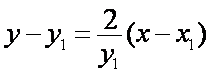
整理,得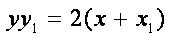
且C点坐标为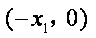
同理得切线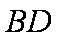
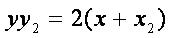
且D点坐标为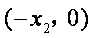
由①②消去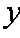
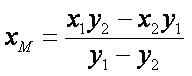
又直线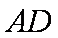
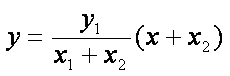
直线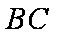
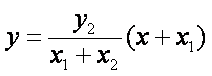
由③④消去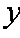
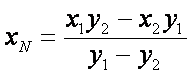
所以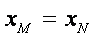
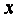
(3)由题意,设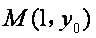
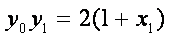
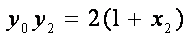
所以
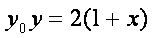
所以直线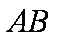
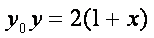
故直线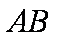
知识点
设




(1)求该抛物线的标准方程。
(2)过Q的直线与抛物线的另一交点为R,与
正确答案
见解析。
解析
(1)∵ ·=0,则x1x2+y1y2=0,--------------------------1分
又P、Q在抛物线上,故y12=2px1,y22=2px2,故得
+y1y2=0, y1y2=-4p2

又|x1x2|=4,故得4p2=4,p=1。
所以抛物线的方程为: 
(2)设直线PQ过点E(a,0)且方程为x=my+a
联立方程组
消去x得y2-2my-2a=0
∴ 
设直线PR与x轴交于点M(b,0),则可设直线PR方程为x=ny+b,并设R(x3,y3),
同理可知,

由①、②可得
由题意,Q为线段RT的中点,∴ y3=2y2,∴b=2a分
又由(Ⅰ)知, y1y2=-4,代入①,可得
-2a=-4 ∴ a=2,故b=4。-----------------------9分
∴
∴

当n=0,即直线PQ垂直于x轴时|PR|取最小值
知识点
如图,过抛物线
(1)求
(2)若

正确答案
见解析
解析
(1)因为


所以

同理

因为

(2)由⑴知






所以

令




因为

记






知识点
如图6,已知点



(1)求
(2)已知抛物线C的顶点为原点O,焦点在
正确答案
见解析。
解析
(1)
设点
于是
当且仅当A、P、B三点共线是取等号,
这时|PA|+|PB|取得最小值
(2)解法一:依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
过点M作y轴的垂线,垂足为G,则点G平分DE,
设圆心为M(m,n),
则
即当M运动时,弦DE的长不随圆心M的变化而变化,
又∵点A'到y轴的距离不变,∴三角形A'DE的面积不随圆心M的变化而变化,
解法二:依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
设圆的圆心为
∴圆的方程为
令
∵点

设
则

即当M运动时,弦DE的长不随圆心M的变化而变化,
又∵点A'到y轴的距离不变,∴三角形A'DE的面积不随圆心M的变化而变化;
解法三:依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
设圆的圆心为
∴圆的方程为
令
∵点

设
由求根公式得

∴当M运动时,弦长|DE|为定值,
又∵点A'到y轴的距离不变,∴三角形A'DE的面积不随圆心M的变化而变化,
解法四:依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
设圆的圆心为
∴圆的方程为
令
设
则
又∵点

∴当M运动时,弦长|DE|为定值,又∵点A'到y轴的距离不变,
∴三角形A'DE的面积不随圆心M的变化而变化,
知识点
已知抛物线

(1)若


(2)是否存在垂直于


正确答案
见解析。
解析
(1)由焦点为

则
所以线段AP的垂直平分线的方程为
令
(当且仅当
即
(2)假设存在所求直线为
AP的中点M(圆心)到
半径为
弦长
若
检验

知识点
如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切,过原点作倾斜角为
(1)求圆M和抛物线C的方程;
(2)设G,H是抛物线C上异于原点O的两个不同点,且
(3)在抛物线C上是否存在两点P,Q关于直线m:y=k(x﹣1)(k≠0)对称?若存在,求出直线m的方程,若不存在,说明理由。
正确答案
见解析。
解析
(1)∵
∴所求抛物线的方程为y2=4x
∴设圆的半径为r,则
(2)设G(x1,y1),H(x2,y2),由

∵

∴x1x2=16,
∵

∴








=

≥


=256
∴
∴△GOH面积最小值为16.
(3)设P(x3,y3),Q(x4,y4)关于直线m对称,且PQ中点D(x0,y0)
∵P(x3,y3),Q(x4,y4)在抛物线C上,
∴

两式相减得:(y3﹣y4)(y3+y4)=4(x3﹣x4)
∴y3+y4=4•

∴y0=﹣2k
∵D(x0,y0)在m:y=k(x﹣1)(k≠0)上
∴x0=﹣1<0,点D(x0,y0)在抛物线外
∴在抛物线C上不存在两点P,Q关于直线m对称
知识点
已知抛物线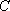
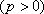
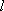
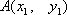
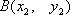
(1)当直线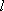
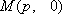
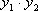
(2)当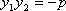
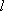
(3)如果直线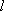
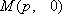
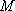
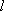
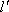
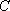
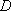
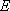
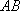
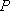
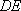
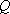
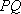
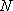
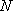
正确答案
见解析
解析
解析:(1)
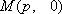
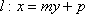
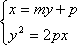
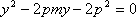
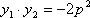
(2)当直线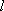
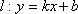
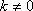
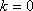
由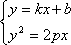
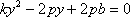
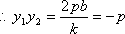
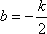
从而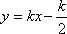
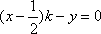
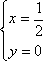
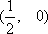
当直线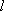
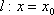
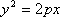
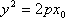
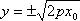
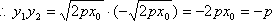
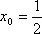
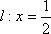
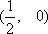
综上所述,当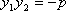
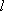
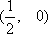
(3)依题意直线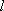
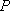
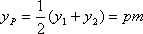
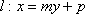
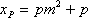
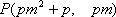
由于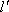
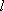
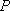
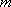
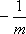
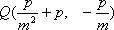
设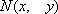
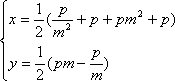
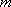
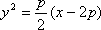
由抛物线的定义知存在直线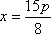
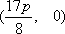
知识点
如图,设D是图中边长为4的正方形区域,E是D内函数
正确答案
解析



知识点
某大型客机承担相距3000公里的甲、乙两地间的客运任务,客机飞行成本由燃料费用和其它费用组成,已知该客机每小时的燃料费用(元)与其飞行速度的平方成正比(比例系数为0.05),其它费用为每小时32000元,且该客机的最大飞行速度为1500公里/小时,在客机全程都是匀速行驶的(假设)条件下。
(1)请将从甲地到乙地的飞行成本

(2)要使从甲地到乙地的飞行成本最少,该客机应以多大的速度飞行?
正确答案
见解析
解析
(1)由题意,每小时的燃料费用为

从甲地到乙地所用的时间为
则从甲地到乙地的飞行成本

即或

(2)由(1)
当且仅当

故客机应以800公里/小时的速度飞行时,能使飞行成本最少,………(14分)
知识点
扫码查看完整答案与解析