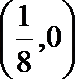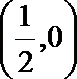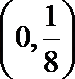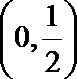- 抛物线及其性质
- 共507题
2．抛物线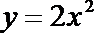
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．已知双曲线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知抛物线
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．抛物线
A
B
C2
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
16．对b>a>0，取第一象限的点Ak（xk，yk）（k=1，2，…，n），使a，x1，x2，…，xn，b成等差数列，且a，y1，y2，…，yn，b成等比数列，则点A1，A2，…，An与射线L：y=x（x>0）的关系为 （ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．方程
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．抛物线的顶点在原点，对称轴是x轴，抛物线上点（-5，m）到焦点距离是6，则抛物线的方程是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4.已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( ).
A2
B3
C
D
正确答案
解析
如图,由抛物线定义知点P到x=-1的距离
即|PF|,由图知|PF|与点P到l1的距离之和的最小值
即点F到直线l1的距离,故最小值
故选A.
知识点
13.已知点P在抛物线y2=4x上,那么点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为______.
正确答案
(
解析
定点Q(2,-1)在抛物线内部,由抛物线的定义知,动点P到抛物线焦点的距离等于它到准线的距离,问题可以转化为当点P到点Q的距离和点P到抛物线的准线距离之和最小时,求点P的坐标,显然当点P是直线y=-1和抛物线y2=4x的交点时,两个距离之和取得最小值,解得这个点的坐标是(
知识点
6.已知圆P:x2+y2=4y及抛物线S:x2=8y,过圆心P作直线 l,此直线与上述两条曲线的四个交点,自左向右顺次记为A,B,C,D,如果|AB|,|BC|,|CD|按此顺序构成一个等差数列,则直线l的斜率为( ).
A±
B
C±
D
正确答案
解析
由题意可知,圆P的圆心坐标为(0,2),半径为2,抛物线S的焦点为(0,2),准线方程为y=-2,画出图象如图所示,其中|BC|=4.由于|AB|,|BC|,|CD|成等差数列,所以|AB|+|CD|=8,所以|AB|+|BC|+|CD|=12,则所求问题等价于当过抛物线S的焦点的直线被抛物线所截得的线段的长度为12时,求直线的斜率.设A(x1,y1),D(x2,y2),过A,D分别向抛物线的准线作垂线,垂足分别为A',D'.根据抛物线定义得|AP|=|AA'|=y1+2,|DP|=|DD'|=y2+2,所以|AD|=|AP|+|DP|=y1+y2+4=12,得y1+y2=8.由题意可知,直线l的斜率存在,且不为0.设直线l的斜率为k(k≠0),则直线l的方程为y=kx+2,即x=
知识点
扫码查看完整答案与解析