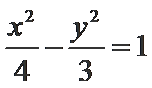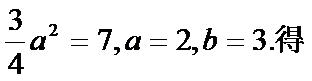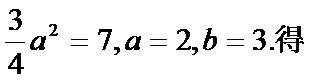- 抛物线及其性质
- 共507题
2.将两个顶点在抛物线y2=2px(p>0)上,另一个顶点是此抛物线焦点的正三角形个数记为n,则( ).
正确答案
解析
如图所示,A,B两点关于x轴对称,
点F的坐标为(
则由抛物线定义,知|AF|=|AA1|,
即m+
又|AF|=|AB|=
∴m+
整理得
∴Δ=
∴方程①有两个不同的实根,
记为m1,m2,且m1+m2=7p>0,
∴m1>0,m2>0,∴n=2.
知识点
2.以抛物线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,椭圆C:

(1) 求椭圆C及抛物线C1、C2的方程;
(2) 若动直线l与直线OP垂直,且与椭圆C交于不同两点M、N,已知点

正确答案
(1) 由题意得A(a,0),B(0,
∴ 抛物线C1的方程可设为
由
代入
∴ 椭圆方程为

(2)由题意可设直线l的方程为
由
由
设M(x1,y1),N(x2,y2),则
∵
∴
∵
∴ 当
解析
解析已在路上飞奔,马上就到!
知识点
10.已知双曲线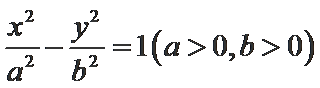
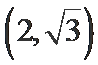
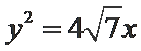
正确答案
解析
将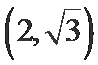
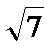
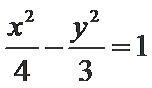
考查方向
解题思路
本题考查运用双曲线的渐近线方程及抛物线的准线方程,求a,b,解题步骤如下:将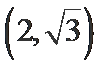

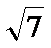
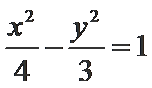
易错点
本题必须注意审题,忽视则会出现错误。
知识点
1.设抛物线的顶点在原点,准线方程为
正确答案
解析
∵抛物线的顶点在原点,准线方程为
∴可设抛物线的方程为
∵
∴
∴抛物线的方程为
考查方向
本题考查抛物线标准方程,考查学生基础知识的掌握能力,属于容易题.
易错点
1.对
知识点
5.如图所示,酒杯的杯体轴截面是抛物线x2=2py (p>0)的一部分,若将半径为r(r>0)的玻璃球放入杯中,可以触及酒杯底部(即抛物线的顶点),则r的最大值为( )
正确答案
解析
本题属于圆锥曲线中的基本问题,题目的难度是逐渐由易到难。
(1)直接按照步骤来求
(2)要注意对参数的讨论
(3)涉及恒成立问题,转化成求二次函数的最值,这种思路是一般解法,往往要利用对称轴.
考查方向
本题主要考查了抛物线与圆的位置关系,在近几年的各省高考题出现的频率较低。
解题思路
无
易错点
本题易在判断线是否在面上发生错误。
知识点
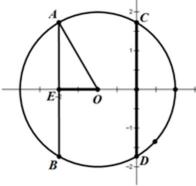
15.已知圆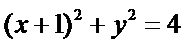

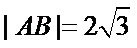
正确答案
8
解析
在平面直角坐标系中画出圆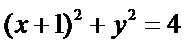
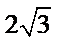
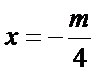
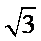
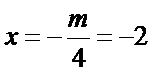
考查方向
解题思路
根据题意画出合适的图形,然后结合图形进行分析和计算.
易错点
本题必须要对抛物线的标准方程和几何性质有深刻的认识,否则容易因为误认为准线为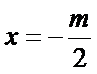
知识点
20. 已知F(







(Ⅰ)求抛物线方程和N点坐标;
(Ⅱ)判断直线




正确答案
见解析
解析
(Ⅰ)由题意

故抛物线方程为
由|NF|=

∵
∴
所以N(2,2)。
(Ⅱ)由题意知直线的斜率不为0,则可设直线

联立方程组

设两个交点A(





由

此时,
故直线


因为M(2,-2),
所以M,E所在直线平行x轴,
所以△MAB的面积



考查方向
解题思路
建立适当的坐标系,利用直线斜率之间的关系建立方程,进而求解,与抛物线联立成方程组,整理可得。
易错点
计算能力弱,找不到面积最小时候的情况
知识点
5.抛物线




正确答案
解析
知识点
扫码查看完整答案与解析