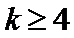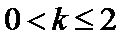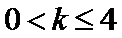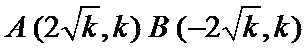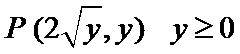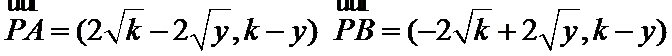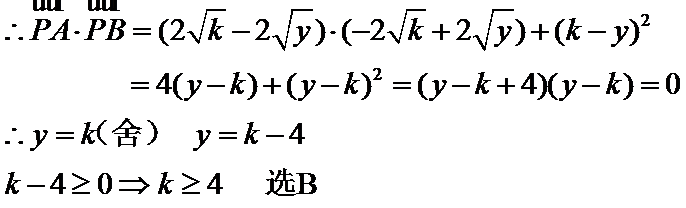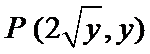- 抛物线及其性质
- 共507题
15.已知抛物线



正确答案
2
解析
由抛物线定义,
所以
所以,

应填2.
考查方向
解题思路
本题主要考查抛物线的定义及抛物线的标准方程等知识,
解题步骤如下:
由抛物线定义求出P点坐标;
由三角形面积公式,求出结果。
易错点
不能根据定义正确求出P点坐标。
知识点
5. A(
正确答案
解析
将A(

考查方向
解题思路
线将A点坐标代入抛物线x2=2py(p>0),求得p值,再结合点到焦点的距离公式求得。
易错点
由抛物线的标准方程没搞清焦点位置,以至于点到焦点的距离公式用错。
知识点
6.已知双曲线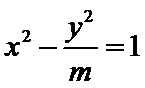
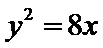

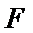
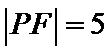
正确答案
解析
因为P在抛物线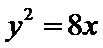
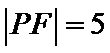
所以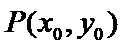
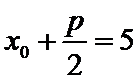
所以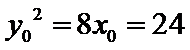
解得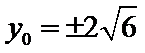
将P点坐标带入,可得m=3,
所以渐近线方程为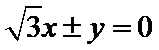
所以选C.
考查方向
解题思路
以PF等于5为突破口,建立方程,求出m的值,进而求出双曲线的渐近线方程
易错点
建立方程后,解方程错误
知识点
6.如果










正确答案
解析
由抛物线方程知p=2,结合焦半径公式|PF|=


考查方向
解题思路
因为|PF|=

易错点
1,由抛物线标准方程求不出P;
2、不能正确掌握抛物线的焦半径公式。
知识点
9.已知F是抛物线y2=4x的焦点,点A,B在该抛物线上且位于x轴的两侧,OA⊥OB(其中O为坐标原点),则△AOB与△AOF面积之和的最小值是( )
正确答案
解析
设直线AB的方程为:x=ty+m,
点A(x1,y1),B(x2,y2),直线AB与x轴的交点为M(m,0),
x=ty+m代入y2=4x,可得y2﹣4ty﹣4m=0,
根据韦达定理有y1•y2=﹣4m,
∵OA⊥OB, ∴

∴x1•x2+y1•y2=0,从而(

∵点A,B位于x轴的两侧,
∴y1•y2=﹣16,故m=4.
不妨令点A在x轴上方,则y1>0,
又F(1,0),
∴S△ABO+S△AFO=




当且仅当


∴△ABO与△AFO面积之和的最小值是8
故选:C.
考查方向
解题思路
1、先设直线方程和点的坐标,联立直线与抛物线的方程得到一个一元二次方程,再利用韦达定理及

易错点
1、设直线方程时未考虑到斜率是否存在而出错。2、再把S△ABO+S△AFO转化成坐标形式时容易出错。
知识点
抛物线

正确答案
解析
根据抛物线





考查方向
本题主要考查了抛物线准线的定义与双曲线的渐近线的定义的综合应用
易错点
容易记错抛物线准线的定义
知识点
10.已知抛物线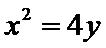
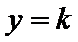
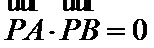
正确答案
解析
抛物线与直线y=k联立确定AB两点的坐标
设动点
则
考查方向
解题思路
本题属于多知识迁移题,需要对知识进行有效转换
(1)确定AB两点的坐标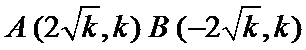
(2)向量
(3)利用向量的数量积运算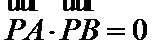
易错点
该题主要易错于题意理解错误,不能有效进行知识的转换
知识点
2. 抛物线

正确答案
解析
抛物线

考查方向
本题主要考查了抛物线的几何性质,属于简单题,是高考的热点,解决此类题的关键是记住抛物线的准线方程。
易错点
本题易在记忆抛物线的准线方程出错。
知识点
13.抛物线








正确答案
解析
设抛物线

则
∵直线


∴可设直线

联立直线

消
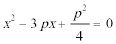
又∵
∴
∴抛物线方程为
考查方向
本题考查抛物线的简单性质,考查数形结合能力,注意解题方法的积累,属于中档题
解题思路
通过设抛物线

可得直线

联立直线方程和抛物线方程,
消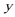
易错点
无
知识点
如图,已知抛物线




















给出下列三个结论:
① 数列
② 对任意

③ 若


所有正确结论的序号是_____.
正确答案
① ② ③
解析
由题意,知数列







考查方向
本题主要考查抛物线的性质与数列的综合应用
易错点
抛物线性质与数列的结合处
知识点
扫码查看完整答案与解析