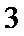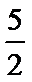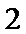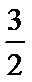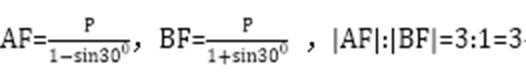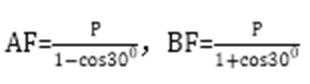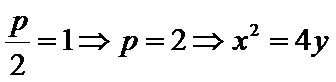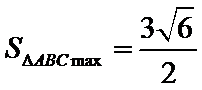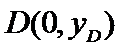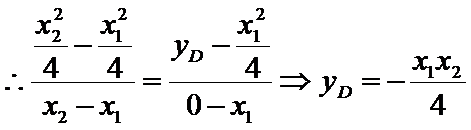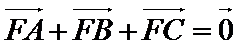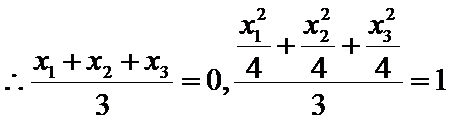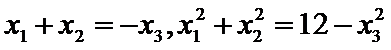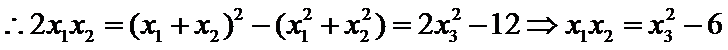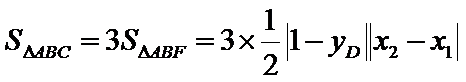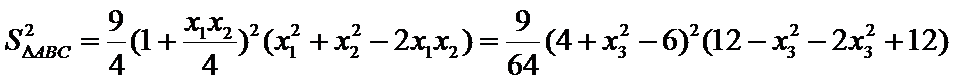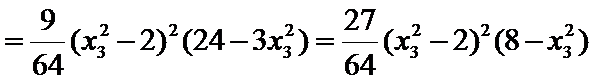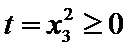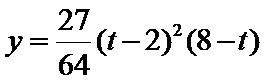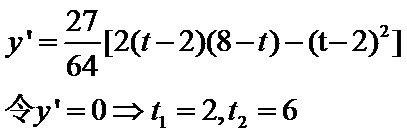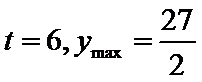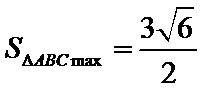- 抛物线及其性质
- 共507题
5.如图,设抛物线


正确答案
解析
试题分析:如图作出抛物线的准线,经过A、B分别向准线作垂线,利用三角形相似
和抛物线的性质,求出三角形面积的比值。
作抛物线的准线x=-1,经过A、B分别向准线作垂线,垂足分别为E,D,与y轴分别
交于N,M,由抛物线的定义可知|BF|=|BD|,|AF|=|AE,|BM||=|BD|-1=|BF|-1,
|AN||=|AE|-1=|AF|-1,∴
考查方向
解题思路
作出抛物线的准线,经过A、B分别向准线作垂线,利用三角形的面积公
式,把三角形面积的比值利用三角形相似进行转化.
易错点
注意正确求出抛物线的准线.
知识点
7.已知双曲线

正确答案
解析
利用抛物线的性质得出焦点为
所以双曲线方程为

考查方向
解题思路
1、利用抛物线的性质得出焦点为
2、根据双曲线的几何性质得出
3、根据双曲线的几何性质直接写出渐近线
易错点
本题主要易错于焦点位置的判断以及m的含义
知识点
6.已知点



正确答案
解析
如图:注意点Q的位置
根据题意得知
选C
考查方向
解题思路
1)把
2)利用不等式的性质直接得出结果
易错点
主要易错于
知识点
10.设直线l与抛物线

正确答案
解析
不妨设直线




代入


可得


考查方向
解题思路
先设直线方程后代人消元得到判别式






易错点
1.不会转化题中给出的条件这样的直线l恰有4条;
找不到r和t之间的关系导致没有思路。
知识点
14.若抛物线C:

正确答案


解析
直线

























考查方向
解题思路
1)根据直线过定点和抛物线的方程判定位置关系;
2)设出与直线
3)利用点到直线的距离进行求解.
易错点
本题易在讨论

知识点
如图所示,椭圆C1:+=1(a>b>0)的离心率为,x轴被曲线C2:y=x2-b截得的线段长等于C1的短轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,直线MA,MB分别与C1相交于点D,E.
24.求C1,C2的方程
25.求证:MA⊥MB;
26. 记△MAB,△MDE的面积分别为S1,S2,若=λ,求λ的取值范围.
正确答案
C1的方程:+y2=1;C2的方程:y=x2-1
解析
由题意,知=,所以a2=2b2. ……1分
又2=2b,得b=1. ……2分
所以曲线C2的方程:y=x2-1,椭圆C1的方程:+y2=1. ……3分
考查方向
主要考查直线与圆锥曲线的综合应用能力,具体涉及到抛物线的方程,椭圆的方程,直线与圆锥曲线的相关知识. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.
解题思路
根据题意直接列出a,b,c方程, 可求出两条曲线的方程
易错点
易在运算中出错,在转化直线与圆锥曲线关系过程中,易在切入点出错
正确答案
略
解析
证明 设直线AB:y=kx,A(x1,y1),B(x2,y2),由题意,知M(0,-1).
则⇒x2-kx-1=0, ……4分
则x1·x2=-1,x1+x2=k,

所以MA⊥MB. ……7分
考查方向
解题思路
设直线方程、交点坐标. 通过向量的数量积等于零, 证明两条线互相垂直
易错点
易在运算中出错,在转化直线与圆锥曲线关系过程中,易在切入点出错
正确答案
[,+∞)
解析
解: 设直线MA的方程:y=k1x-1,直线MB的方程:y=k2x-1,……8分
由25题知k1k2=-1,M(0,-1),
由解得或 ……9分
所以A(k1,k-1).同理,可得B(k2,k-1).……10分
故S1=|MA|·|MB|=·|k1||k2|.
由解得或
所以D(,).同理,可得E(,).……11分
故S2=|MD|·|ME|=·,
=λ==≥,……13分
则λ的取值范围是[,+∞).……14分
考查方向
主要考查直线与圆锥曲线的综合应用能力,具体涉及到抛物线的方程,椭圆的方程,直线与圆锥曲线的相关知识. 本小题对考生的化归与转化思想、运算求解能力都有很高要求.
解题思路
设MA,MB的方程,通过与抛物线,椭圆联立方程组,解出A,B,D,E的坐标,然后分别用



易错点
易在运算中出错,在转化直线与圆锥曲线关系过程中,易在切入点出错
已知抛物线









23.求
24.若圆




正确答案
(1)抛物线

解析
试题分析: 本题属于抛物线、直线、圆的方程及位置关系考查题型,意在考查考生的分析问题、解决问题的能力及运算能力。
(Ⅰ)设

又∵以


∴




考查方向
解题思路
(1)直线








(2)通过直线

易错点
以


正确答案
(2)直线

圆
解析
试题分析: 本题属于抛物线、直线、圆的方程及位置关系考查题型,意在考查考生的分析问题、解决问题的能力及运算能力。
(Ⅱ)设直线


化简整理得
∴


∴圆心

∵圆


∴
∴

此时直线


圆心

圆

考查方向
解题思路
(1)直线








(2)通过直线

易错点
以


4.已知抛物线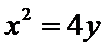
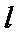
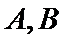
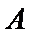
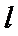
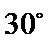
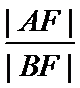
正确答案
解析
考查方向
解题思路
根据题意, 直接用焦半径表示AF与BF的长度.
易错点
忽略直线过焦点,导致AF与BF的长度无法用3
知识点
14. 已知直线l:y=kx+t号圆:x2 +(y+l)2 =1相切且与抛物线C:x2 =4y交于不同的两点M,N,则实数t的取值范围是____.
正确答案
解析
因为直线与圆相切





考查方向
解题思路
先利用直线与圆相切找到k与t之间的关系,再通过直线与抛物线有两个不同的交点求出t的取值范围。
易错点
直线中有两个变量,如何把k转化或者求出。
知识点
已知点F(0,1)为抛物线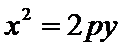
24.求抛物线C的方程;
25.点A、B、C是抛物线上三点且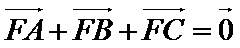
正确答案
(1)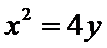
解析
(1)由题意知
考查方向
解题思路
1)第一问利用抛物线的定义,可求出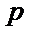
2)第二问首先设出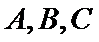
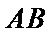
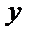
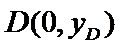
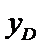
易错点
错位相减法求和计算容易错。
正确答案
(2)
解析
(2)令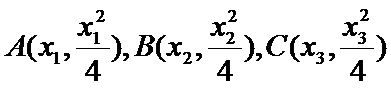
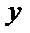
又因为
从而
令
当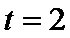
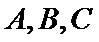
当
考查方向
解题思路
1)第一问利用抛物线的定义,可求出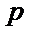
2)第二问首先设出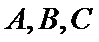
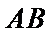
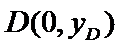
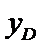
易错点
错位相减法求和计算容易错。
扫码查看完整答案与解析