抛物线及其性质_章节学习

1

题型：单选题

|

单选题 · 5 分

11.已知是抛物线的焦点，为抛物线上的动点，且的坐标为，则

的最小值是（）

A

B

C

D

正确答案

C

解析

由题意知，，设，由抛物线的定义知，，所以，当时，，因为，所以，当x=0时，，综上所述，的最小值是，故选C选项。

考查方向

本题主要考查圆锥曲线的定义、基本不等式求最值等知识，意在考查考生的转化能力和构建函数的意识。

解题思路

1.先根据题意构造函数，2.利用基本不等式求函数的最值。

易错点

1.不会构建函数；2.不会求的最值。

知识点

抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

1

题型：填空题

|

填空题 · 4 分

12.过抛物线：的焦点作直线交抛物线于两点，若，则抛物线的顶点到直线的距离为 ▲ ．

正确答案

解析

设为直线的倾斜角，不妨设直线AB的位置如图，由抛物线方程可知，p=4,|AF|= ，所以= 所以sin= ,在三角形OHF中，|OH|=|OF|sin=2= .

考查方向

抛物线的焦半径公式，直线与抛物线的位置关系，数形结合的解题方法，技巧

解题思路

先通过焦半径, 算出直线AB的倾斜角, 再利用数形结合的方法, 计算顶点到直线AB的距离

易错点

忽略AB是焦点弦, 找不到恰当的解题方法

知识点

抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

1

题型：填空题

|

填空题 · 5 分

14.已知抛物线与经过该抛物线焦点的直线在第一象限的交点为在轴和准线上的投影分别为点，则直线的斜率为

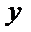
正确答案

2

解析

如图，由题意可得 AF=AC设AF=3m，由AB=2BC，可AB=2m,BC=m，过A作AD垂直x轴于D，设A的横坐标为则3m=1+=2m,所以m=1,A(2,2)，F(1,0),所以直线AF的斜率为2

考查方向

本小题考查直线与抛物线的位置关系

解题思路

画出抛物线简图，用抛物线定义，结合题中的位置关系，数量关系，求出点A(2,2)，既然得到直线AF的斜率为2

易错点

对抛物线定义及性质掌握不熟

知识点

抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 12 分

．

23.求抛物线的方程；

24.已知动圆的圆心在抛物线上，且过定点，若动圆与轴交于、两点，求的最大值．

第(1)小题正确答案及相关解析

正确答案

（1）；

解析

(1) 设抛物线的焦点为，则直线，

由，得 -------------2分

，，，

抛物线的方程为 ------------4分

考查方向

本题考查了抛物线过焦点的弦长的求解及基本不等式的应用

解题思路

联立直线与抛物线方程,求解抛物线过焦点的弦长.

设动圆圆心 ,表示出圆的方程并求出A，B点，用距离公式表示，即可得到结果。

易错点

联立消元计算出错

第2问计算量较大，对学生的运算能力是个严重的考验。

不能正确地两次利用基本不等式求最值。

第(2)小题正确答案及相关解析

正确答案

（2）

解析

设动圆圆心，则，

且圆，

令，整理得：，

解得：， -------------4分

设，

当时，，①

当时，，，，

，且，②

综上①知， -------------8分

在单调递减，

，

当且仅当，即时等号成立．

所以的最大值为． -------------12分

考查方向

本题考查了抛物线过焦点的弦长的求解及基本不等式的应用

解题思路

联立直线与抛物线方程,求解抛物线过焦点的弦长.

设动圆圆心 ,表示出圆的方程并求出A，B点，用距离公式表示，即可得到结果。

易错点

联立消元计算出错

第2问计算量较大，对学生的运算能力是个严重的考验。

不能正确地两次利用基本不等式求最值。

1

题型：简答题

|

简答题 · 16 分

已知抛物线，为抛物线上的点，若直线经过点且斜率为，则称直线为点的“特征直线”. 设、为方程（）的两个实根，记.

24.求点的“特征直线”的方程；

25.已知点在抛物线上，点的“特征直线”与双曲线经过二、四象限的渐进线垂直，且与轴的交于点，点为线段上的点. 求证：；

26.已知、是抛物线上异于原点的两个不同的点，点、的“特征直线”分别为、，直线、相交于点，且与轴分别交于点、. 求证：点在线段上的充要条件为（其中为点的横坐标）.

第(1)小题正确答案及相关解析

正确答案

（1）.；

解析

（1）由题意的斜率为1，

所以点的“特征直线”的方程为.

考查方向

本题主要考查圆锥曲线的的定义、性质、直线与圆锥曲线的位置关系、充要条件等知识，意在考查考生的理解能力，转化与划归的能力。

解题思路

1根据题意直接求出“特征直线”的方程为.

易错点

1.不理解特征直线的定义导致无法入手；2.证明充要条件时不知道应该证明充分性和必要性。

第(2)小题正确答案及相关解析

正确答案

（1）.；

解析

设点，由于双曲线所求渐进线的斜率为

所以，进而得

线段的方程为

所以满足

所对应方程为：，解得，

因为，所以，进而

考查方向

本题主要考查圆锥曲线的的定义、性质、直线与圆锥曲线的位置关系、充要条件等知识，意在考查考生的理解能力，转化与划归的能力。

解题思路

线根据渐近线方程求出，进而得到点（a,b）满足的方程；

易错点

1.不理解特征直线的定义导致无法入手；2.证明充要条件时不知道应该证明充分性和必要性。

第(3)小题正确答案及相关解析

正确答案

见解析

解析

(3)设，，则、的方程分别为

，，

解、交点可得，，

所对应的方程为：，

得

必要性：因为点在线段上，所以

当时，，得，

所以，进而

① 充分性：由，得，

当时，，得，

当时，得，得，

所以点在线段上.

综上，点在线段上的充要条件为

考查方向

本题主要考查圆锥曲线的的定义、性质、直线与圆锥曲线的位置关系、充要条件等知识，意在考查考生的理解能力，转化与划归的能力。

解题思路

先证明结论的充分性，后证明其必要性。

易错点

1.不理解特征直线的定义导致无法入手；2.证明充要条件时不知道应该证明充分性和必要性。

1

题型：简答题

|

简答题 · 13 分

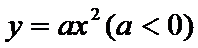
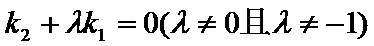
抛物线C的方程为，过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1),B(x2,y2)两点(P,A,B三点互不相同)，且满足.

24.求抛物线C的焦点坐标和准线方程；

25.设直线AB上一点M，满足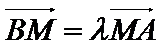，证明线段PM的中点在y轴上；

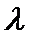
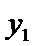
26.当=1时，若点P的坐标为（1，-1），求∠PAB为钝角时点A的纵坐标的取值范围.

第(1)小题正确答案及相关解析

正确答案

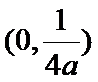
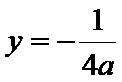
（1）焦点坐标为，准线方程为；

解析

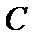
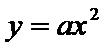
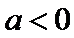
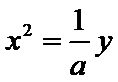
（Ⅰ）由抛物线的方程（）得，,

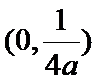
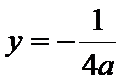
焦点坐标为，准线方程为．

考查方向

本题主要考查抛物线的几何性质，直线与圆锥曲线的位置关系等知识，意在考查考生的运算求解能力和综合解决问题的能力。

解题思路

根据抛物线的几何性质直接得到即可；

易错点

无

第(2)小题正确答案及相关解析

正确答案

（2）略；

解析

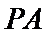
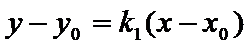
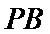
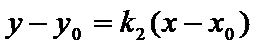
（Ⅱ）证明：设直线的方程为，直线的方程为．

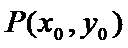
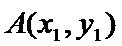
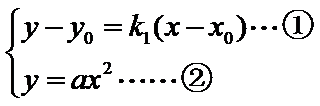
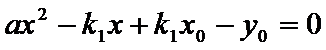
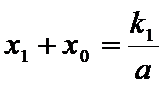
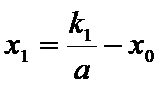
点和点的坐标是方程组的解．将②式代入①式得，于是，故　③

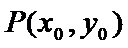
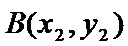
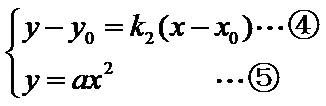
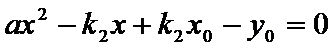
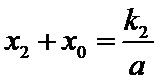
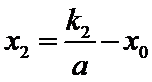
又点和点的坐标是方程组的解．将⑤式代入④式得．于是，故．

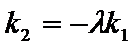
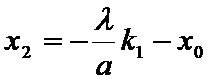
由已知得，，则．　　⑥----------------6分

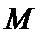
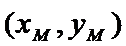
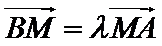
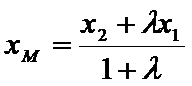
设点的坐标为，由，则．

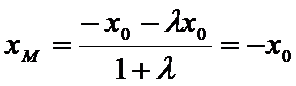
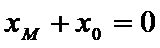
将③式和⑥式代入上式得，即．

∴线段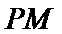的中点在轴上．-

考查方向

本题主要考查抛物线的几何性质，直线与圆锥曲线的位置关系等知识，意在考查考生的运算求解能力和综合解决问题的能力。

解题思路

1

先根据条件求出A,B的横坐标后带入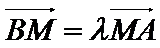求出M的横坐标即可得到答案；

易错点

不会求解点A,B的坐标，运算量大；

第(3)小题正确答案及相关解析

正确答案

（3）

解析

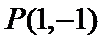
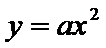
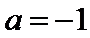
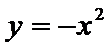
（Ⅲ）因为点在抛物线上，所以，抛物线方程为．

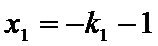
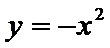
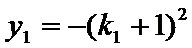
由③式知，代入得．

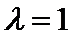
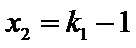
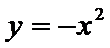
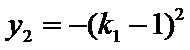
将代入⑥式得，代入得．

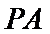
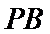
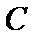
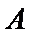
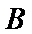
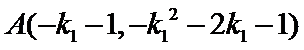
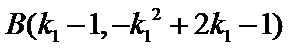
因此，直线、分别与抛物线的交点、的坐标为

，．

于是，，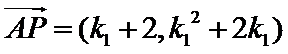

．

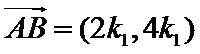
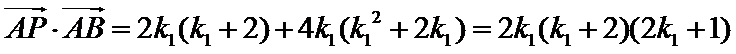
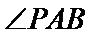
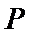
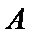
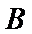
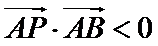
因为钝角且、、三点互不相同，故必有．

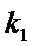
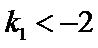
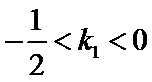
求得的取值范围是或．

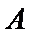
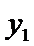
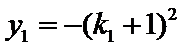
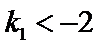
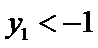
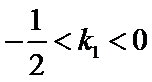
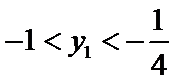
又点的纵坐标满足，故当时，；当时，．即

考查方向

本题主要考查抛物线的几何性质，直线与圆锥曲线的位置关系等知识，意在考查考生的运算求解能力和综合解决问题的能力。

解题思路

先求出抛物线的方程，然后根据第（2）问求出点A,B的坐标，然后将∠PAB为钝角转化为向量求解即可。

易错点

不会转化题中给出的条件∠PAB为钝角，导致做不出正确答案。

1

题型：填空题

|

填空题 · 5 分

14．如图，探照灯反射镜的纵截面是抛物线的一部分，光源在抛物线的焦点F处，灯口直径AB为0，灯深（顶点O到反射镜距离）0，则光源F到反射镜顶点O的距离为

正确答案

或或

解析

.建立如图平面直角坐标系，设抛物线方程为，

则点A（40，30）在抛物线上，（）

考查方向

本题主要考查抛物线的几何性质等知识，意在考查考查对于抛物线的应用能力和运算求解能力。

解题思路

1.建立平面直角坐标系设出抛物线的方程；

2.根据题意点A（40，30）在抛物线上求出p;

易错点

不会将题中给出的应用问题建立坐标系求解；

知识点

抛物线的定义及应用抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 12 分

已知，抛物线上一点到抛物线焦点的距离为．

24.求和的值；

25.如图5所示，过作抛物线的两条弦和

（点、在第一象限），若，求证：直线经过一个定点．

第(1)小题正确答案及相关解析

正确答案

（1），；

解析

（Ⅰ）由点到抛物线焦点的距离为，结合抛物线的定义得，，即，

抛物线的方程为，把点的坐标代入，可解得；

考查方向

本题主要考查圆锥曲线的性质，直线与圆锥曲线的位置关系等知识，意在考查考生的运算求解能力和综合解决问题的能力。

解题思路

1.先利用抛物线定义求出p,然后将点M的坐标带入求解即可；2.设出直线、的方程后分别与抛物线的方程联立消元导出韦达定理后将表示为方程，后利用韦达定理求解即可得到答案。

易错点

不会利用抛物线的定义转化题中的条件到抛物线焦点的距离为．不知道该如何表示，或运算出错，导致运算越算越乱。

第(2)小题正确答案及相关解析

正确答案

（2）略

解析

（Ⅱ）：显然直线、的斜率都存在，

分别设、的方程为，

联立，得，

设，，，，

则，，同理，，

故

，

注意到点、在第一象限，，∴

故得，，∴，即直线恒经过点．

考查方向

本题主要考查圆锥曲线的性质，直线与圆锥曲线的位置关系等知识，意在考查考生的运算求解能力和综合解决问题的能力。

解题思路

1.先利用抛物线定义求出p,然后将点M的坐标带入求解即可；2.设出直线、的方程后分别与抛物线的方程联立消元导出韦达定理后将表示为方程，后利用韦达定理求解即可得到答案。

易错点

1.不会利用抛物线的定义转化题中的条件到抛物线焦点的距离为．2.不知道该如何表示，或运算出错，导致运算越算越乱。

1

题型：单选题

|

单选题 · 5 分

设抛物线的焦点为，准线为，为抛物线上一点，，为垂足，如果直线斜率为，那么（）

A

B8

C

D16

正确答案

B

解析

如图，由结合直线斜率为知，在中，由抛物线的定义知，所以为等边三角形，在中，由，即，所以答案应为B选项。

考查方向

本题主要考查了抛物线的定义和几何关系,属于比较灵活的题，常考求方程、离心率的值或范围、中点弦，面积等问题。

解题思路

1、由直线斜率为知；2、在中，由抛物线的定义知，所以为等边三角形；3、在中解出的值。

易错点

本题难在定义的应用和几何关系的寻找。

知识点

抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

1

题型：简答题

|

简答题 · 12 分

已知抛物线，过其焦点作斜率为1的直线交抛物线C于M、N两点，且．

23.求抛物线C的方程；

24.已知动圆P的圆心在抛物线C上，且过定点D(0，4)，若动圆P与x轴交于A、B两点，且，求的最小值．

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）

解析

(1) 设抛物线的焦点为，则直线，

由，得 ………………………2分

，，

， ………………………4分

抛物线的方程为 ………………………5分

考查方向

抛物线与圆的定义与几何性质，不等式的应用.

解题思路

过抛物线焦点的弦长运用抛物线的定义可求得；求出的函数表达式，再求最值.

易错点

本题抛物线为开口向上的，故焦点弦长为；求函数的最值时注意定义域.

第(2)小题正确答案及相关解析

正确答案

.

解析

设动圆圆心，则，

且圆，

令，整理得：，

解得：， ………………………7分

，…………9分

当时，，

当时，，，，

，

所以的最小值为． ………………………12分

考查方向

抛物线与圆的定义与几何性质，不等式的应用.

解题思路

过抛物线焦点的弦长运用抛物线的定义可求得；求出的函数表达式，再求最值.

易错点

本题抛物线为开口向上的，故焦点弦长为；求函数的最值时注意定义域.

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点