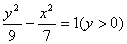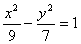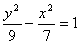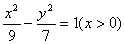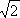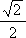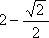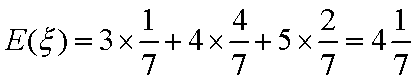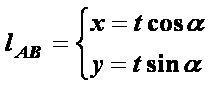- 抛物线及其性质
- 共507题
已知点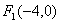
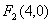
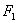
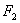
正确答案
解析
略
知识点
在直角坐标系xOy中,直线l过抛物线
正确答案
解析
由





知识点
在极坐标系中,直线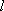
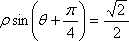
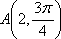
正确答案
解析
略
知识点
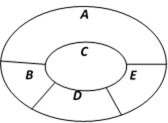
如图,











正确答案
2
解析
连接








又
∴
∴



知识点
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每
②若两个变量的线性相关性越强,则相关系数的绝对值越接近于
③在某项测量中,测量结果







④对分类变量



正确答案
解析
①应为系统(等距)抽样;②线性相关系数






知识点
己知⊙O:x2 +y2=6,P为⊙O上动点,过P作PM⊥x轴于M,N为PM上一点,且
(1)求点N的轨迹C的方程;
(2)若A(2,1),B(3,0),过B的直线与曲线C相交于D、E两点,则kAD+kAE是否为定值?若是,求出该值;若不是,说明理由。
正确答案
见解析
解析
(1)设



由


由于点







(2)设




由







知识点
某中学要用鲜花布置花圃中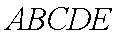
(1)当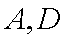
(2)求恰有两个区域用红色鲜花的概率;
(3)记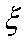
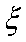
正确答案
见解析
解析
解:(1)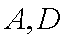
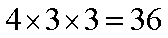
(2)设
当区域
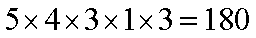
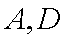
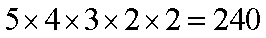



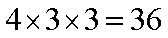
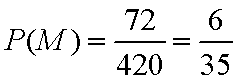
(3)
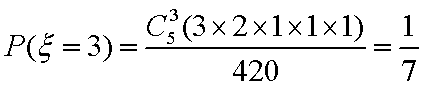
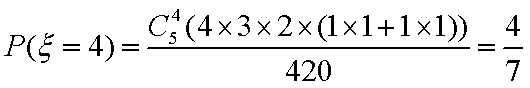
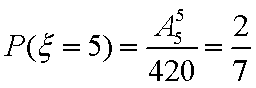
所以分布列为
知识点
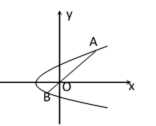
在抛物线y2=4a(x+a)(a>0),设有过原点O作一直线分别
交抛物线于A、B两点,如图所示,试求|OA|•|OB|的最小值。
正确答案
见解析
解析
法一,(极坐标)
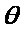
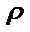

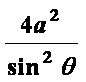
法二:(参数方程)
代入y2=4a(x+a)中得:t2sin2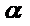
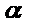
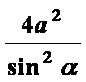
知识点
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示。
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试。
1)已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
2)学校决定在这6名学生中随机抽取2名学生接受考官D的面试,第4组中有

正确答案
见解析
解析
(1) 第三组的频率为0.06
第四组的频率为0.04
第五组的频率为0.02
(2)1)设M:学生甲和学生乙同时进入第二轮面试
P(M)=

2)

知识点
设函数

(1)如果


(2)求实数a的值,使得函数f(x)同时具备如下的两个性质:
① 对于任意实数


② 对于任意实数


正确答案
见解析
解析
(1)函数



依题意,

此时,

因为




所以,函数


因此,当


(2)令

由(1)中的结论可知,


(ⅰ)如果


根据(*)可得

若

于是


(ⅱ)如果



则


于是



综合(ⅰ)(ⅱ)可得,
知识点
扫码查看完整答案与解析