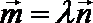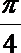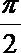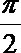- 抛物线及其性质
- 共507题
7.已知点









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 点













正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知复数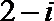
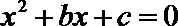
(1)求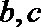
(2)若向量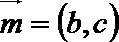
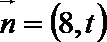
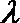
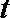
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 过抛物线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 函数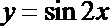

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数f(x)=
(1)试就实数a的不同取值,写出该函数的单调递增区间;
(2)已知当a>0时,函数在(0,

(3)若函数f(x)在区间
正确答案
(1)①当a<0时,函数f(x)的单调递增区间为(﹣

②当0<a≤1时,函数f(x)的单调递增区间为(﹣∞,0)及(0,+∞),
③当a>1时,函数f(x)的单调递增区间为(﹣∞,﹣

(2)由题设及(1)中③知
且a>1,解得a=3,
因此函数解析式为f(x)=
(3)1#当a(a﹣1)>0即a<0或a>1时
由图象知
解得a∈(﹣∞,

2#当a=1时,函数为正比例函数,故在区间内存在反函数,所以a=1成立.
3#当a(a﹣1)<0,得到



综上a∈∈(﹣∞,



解析
解析已在路上飞奔,马上就到!
知识点
3.点


正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
8.设











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知抛物线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析