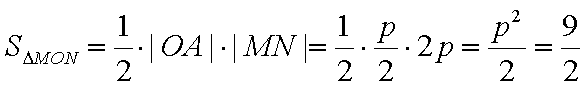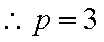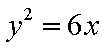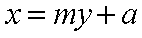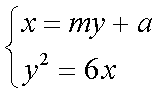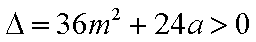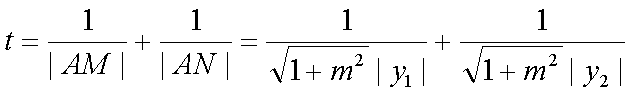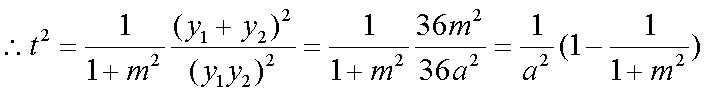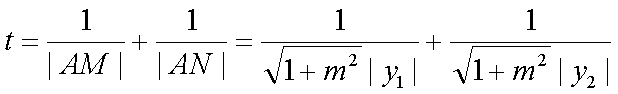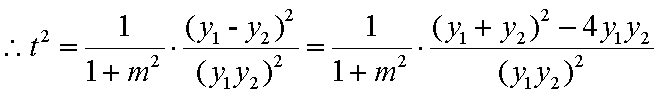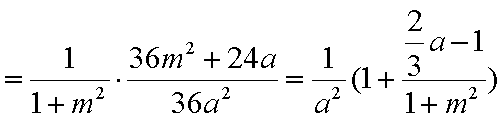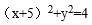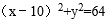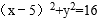- 抛物线及其性质
- 共507题
设抛物线y2=4x上一点P到直线x=-2的距离为5,则点P到该抛物线焦点的距离是
正确答案
4
解析
由抛物线的定义知:点P到抛物线焦点的距离等于点P到准线x=-1的距离,所以点P到该抛物线焦点的距离是5-1=4.
知识点
己知抛物线的参数方程为









正确答案
2
解析
∵





由抛物线得几何性质得



知识点
已知抛物C的标准方程为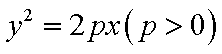

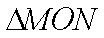
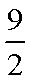
(1)求抛物线C的标准方程;
(2)记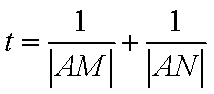
正确答案
见解析
解析
(1)由题意,
抛物线C的方程为
(2) 设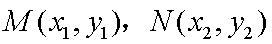
联立
得
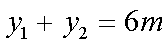
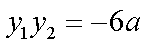
由对称性,不妨设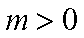
(i)
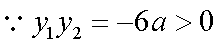
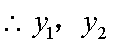
又
不论a取何值,t均与m有关,即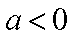
(ii) 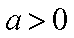
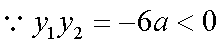
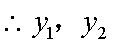
又
所以,仅当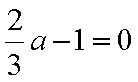
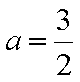
知识点
设顶点在原点,焦点在x轴上的抛物线过点P(2,4),过P作抛物线的动弦PA,PB,并设它们的斜率分别为kPA,kPB。
(1)求抛物线的方程;
(2)若kPA+kPB=0,求证直线AB的斜率为定值,并求出其值;
(3)若kPA·kPB=1,求证直线AB恒过定点,并求出其坐标。
正确答案
见解析。
解析
(1)依题意,可设所求抛物线的方程为y2=2px(p>0),
因抛物线过点(2,4),故42=4p,p=4,抛物线方程为y2=8x。
(2)设A(x1,y1),B(x2,y2),则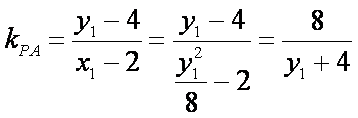
同理
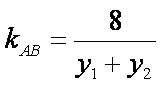
∵kPA+kPB=0,
∴



∴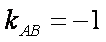
即直线AB的斜率恒为定值,且值为-1。
(3)∵kPAkPB=1,∴

直线AB的方程为
将-y1y2=4(y1+y2)-48代入上式得
(y1+y2)(y+4)=8(x+6),该直线恒过定点(-6,-4),命题得证。
知识点
设抛物线y2=2px(p>0)的焦点为F,其准线与x轴交于点C,过点F作它的弦AB,若∠CBF=90°,则|AF|﹣|BF|= 。
正确答案
2P
解析
设AB方程为:y=k(x﹣

即k2x2﹣(k2+2)px+
设两交点为A(x2,y2),B(x1,y1),∠CBF=90°即(x1﹣

∴ x12+y12=



∴ B(



∵ x1x2=

∴ x2=
∴ A(


∴|AF|﹣|BF|=2P,
故答案为2P。
知识点
已知抛物线




正确答案
解析
抛物线












知识点
如图,直线y=2x与抛物线y=3﹣x2所围成的阴影部分的面积是( )
正确答案
解析
由

∴直线y=2x与抛物线y=3﹣x2交于点A(﹣3,﹣6)和B(1,2)
∴两图象围成的阴影部分的面积为
=(3×1﹣

=
知识点
以抛物线y2=20x的焦点为圆心,且与双曲线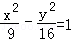
正确答案
解析
由双曲线方程可得a=3,b=4,c=5,
实轴长=6,离心率e=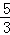
顶点坐标(﹣3,0),(3,0),
焦点坐标(﹣5,0),(5,0),
渐近线方程y=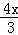
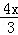
圆心(5,0)到直线4x+3y=0的距离即为所求圆的半径R
R=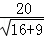
所以圆方程:(x﹣5)2+y2=16。
知识点
已知









(1)求椭圆
(2)直线






正确答案
见解析。
解析
(1)由题意可设椭圆


由题意知


故椭圆


(2)以

证明如下:由题意可设直线

则点




由

设点


所以

因为点

当




直线



当


所以直线

点


又因为

故以

综上得,当直线



知识点
抛物线







正确答案
解析
设


知识点
扫码查看完整答案与解析