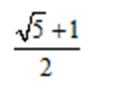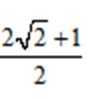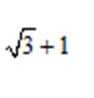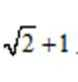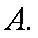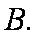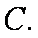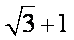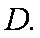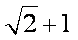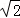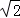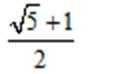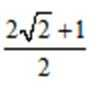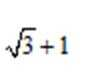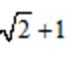- 抛物线及其性质
- 共507题
若抛物线
A
B
C
D
正确答案
解析
焦点坐标
知识点
10.抛物线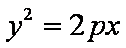
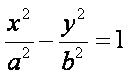
A
B
C
D
正确答案
解析
因为抛物线和双曲线焦点相同，所以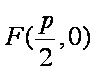
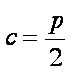
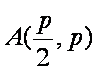
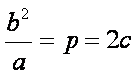
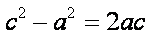
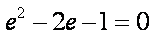
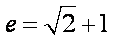
知识点
已知抛物线Γ：y2=4x的焦点为F，P是Γ的准线上一点，Q是直线PF与Γ的一个交点，若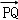
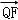
正确答案
x+y﹣1=0或x﹣y﹣1=0
解析
抛物线Γ：y2=4x的焦点F（1，0），设Q到l的距离为d，则|QF|=d
∵
∴|
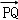
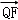
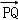
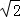
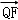
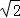
∴直线的倾斜角为45°或135°，
∴直线的斜率为±1，
∴直线的方程为x+y﹣1=0或x﹣y﹣1=0。
故答案为：x+y﹣1=0或x﹣y﹣1=0。
知识点
9.抛物线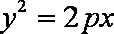
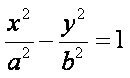
A
B
C
D
正确答案
解析
因为抛物线和双曲线焦点相同，所以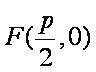
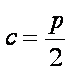
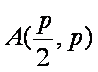
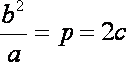
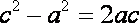
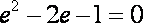
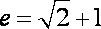
知识点
13.过抛物线
正确答案
2
解析
由题意可知过焦点的直线方程为
知识点
14.已知抛物线方程为
正确答案
解析
略
知识点
正确答案
（0,2）
解析
略
知识点
10.已知抛物线C1：y=
A
B
C
D
正确答案
解析
由抛物线C1：y=
所以抛物线的焦点坐标为F（0，
由
则抛物线的焦点与双曲线的右焦点的连线所在直线方程为
即
设该直线交抛物线于M（
由题意可知
把M点代入①得：
知识点
10.已知抛物线
A
B
C3
D2
正确答案
解析
设
知识点
已知抛物线的方程为
A2
B
C2或
D2或
正确答案
解析
过A作AD⊥x轴于D，令FD=m，则FA=2m，即F到准线的距离为2m，由抛物线的定义可得p+m=2m，即m=p，所以
知识点
扫码查看完整答案与解析