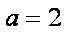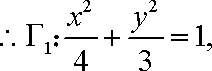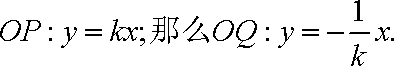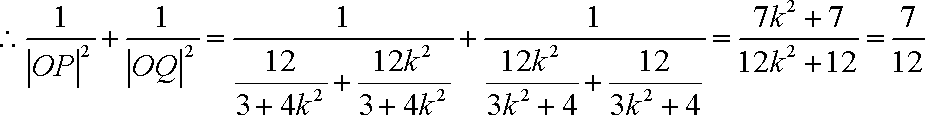- 定积分
- 共55题
已知函数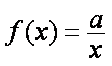
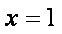
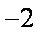
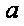
正确答案
2
解析
易得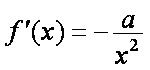
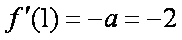
知识点
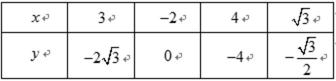
设椭圆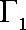
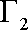

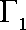
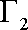
轴上,过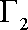
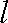
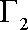
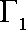
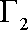
(1)求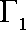
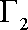
(2)已知
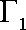
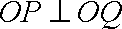
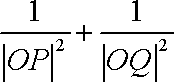
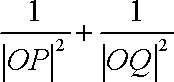
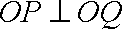
正确答案
见解析
解析
(1)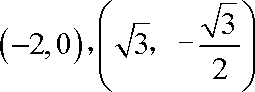
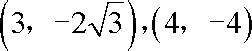

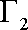
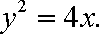
(2)①若P、Q分别为长轴和短轴的端点,则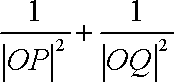
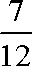
②若P、Q都不为长轴和短轴的端点,
设
联立方程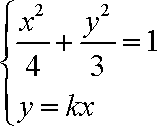
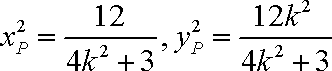

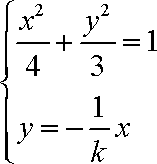
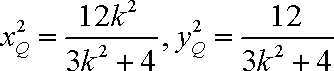
综合①②可知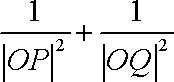
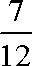
反之,对于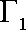

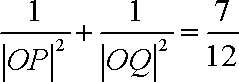
设
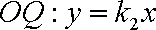
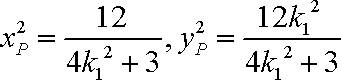
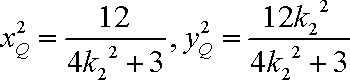
由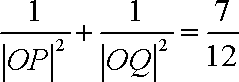
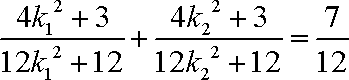
即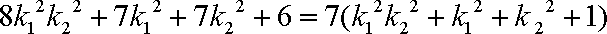
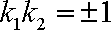
所以当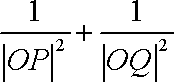
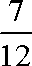
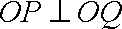
知识点
(1)已知


(2)设数列





证明:对任意的正整数n,
关于
正确答案
见解析
解析
(1)证明:左边
右边
所以
(2)证明:由题意得数列



则

所以对任意的正整数n,

知识点
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD=AD=2。
(1)求PC与平面PBD所成的角;
(2)在线段PB上是否存在一点E,使得PC⊥平面ADE?并说明理由。
正确答案
(1)
解析
(1)连接AC,设AC∩BD=O,连接PO
∵PD⊥平面ABCD,CO⊂平面ABCD∴PD⊥CO
由ABCD为正方形,知CO⊥BD
∵PD∩BD=D∴CO⊥平面PBD
∴∠CPO是直线PC与平面PBD所成的角
在Rt△POC中,
∴
∴直线PC与平面PBD所成的角为
(2)建立如图所示的空间直角坐标系D_xyz,设线段PB上存在一点E,使得PC⊥平面ADE
则存在实数λ,使得
∵P(0,0,2),B(2,2,0)∴
∴

由题意显然有AD⊥平面PCD∴PC⊥AD 要使PC⊥平面ADE,只需
即
∴
故在线段上存在一点E(E为线段的中点)使得PC⊥平面ADE
知识点
已知函数





正确答案
解析
依题意得,函数f(x)的图象关于点(0,0)对称,因此f(x)是奇函数,又函数y=f(x)是定义在R上的增函数,于是不等式f(x2-6x+21)+f(y2-8y)<0,即f(x2-6x+21)<-f(y2-8y)=f(-y2+8y),所以x2-6x+21<-y2+8y,即(x-3)2+(y-4)2<4,该不等式表示的是以(3,4)为圆心,以2为半径的圆内区域。x2+y2=()2可视为动点P(x,y)与原点间的距离的平方,因此问题可转化为不等式组x>3((x-3)2+(y-4)2<4,)表示的平面区域内的所有点与原点间的距离的平方的取值范围,该不等式组表示的平面区域是如图所示的半圆与直线x=3所围成的区域(不含边界),结合图形不难得知,平面区域内的所有的点与原点间的距离的平方应大于原点与点(3,2)间的距离的平方,应小于原点与点(3,4)间的距离再加上2的和的平方,即当x>3时,x2+y2的取值范围是(13,49)。
知识点
扫码查看完整答案与解析