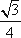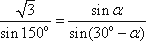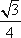- 定积分
- 共55题
为提高学生学习数学的兴趣,某地区举办了小学生“数独比赛”.比赛成绩共有90分,70分,60分,40分,30分五种,按本次比赛成绩共分五个等级,从参加比赛的学生中随机抽取了30
名学生,并把他们的比赛成绩按这五个等级进行了统计,得到如下数据表:
(1)根据上面的统计数据,试估计从本地区参加“数独比赛”的小学生中任意抽取一人,
其成绩等级为“

(2)根据(1)的结论,若从该地区参加“数独比赛”的小学生(参赛人数很多)中任选3人,
记




(3)从这30名学生中,随机选取2人,求“这两个人的成绩之差大于
正确答案
见解析
解析
(1)根据统计数据可知,从这30名学生中任选一人,分数等级为“


从本地区小学生中任意抽取一人,其“数独比赛”分数等级为“


(2)由已知得,随机变量
所以



随机变量
所以
(3)设事件M:从这30名学生中,随机选取2人,这两个人的成绩之差大于
设从这30名学生中,随机选取2人,记其比赛成绩分别为
显然基本事件的总数为
不妨设
当




当



当


所以
所以从这30名学生中,随机选取2人,这两个人的成绩之差大于

知识点
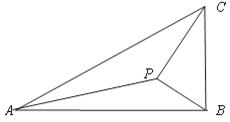
如图,在△ABC中,∠ABC=90°,AB=,BC=1,P为△ABC内一点,∠BPC=90°
(1)若PB=,求PA;
(2)若∠APB=150°,求tan∠PBA
正确答案
(1) 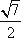
解析
(1)由已知得,∠PBC=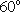
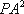
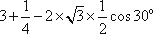

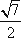
(2)设∠PBA=
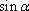

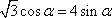
∴
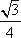

知识点
已知

(1) 求
(2)若存在



正确答案
见解析。
解析
解:(1)定义域为


①当







②当





综合上述,当








(2)由题知,对任意














知识点
(不等式选做题)不等式|2x-1|<|x|+1解集是 。
正确答案
解析
略
知识点
如图,椭圆








(1)求证:
(2)设



正确答案
见解析
解析
(1)设

又

即
(2)
因为O、P、Q三点共线,所以
设直线PQ的斜率为k,则

由①②得

从而

知识点
扫码查看完整答案与解析