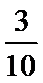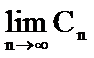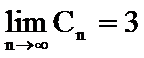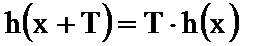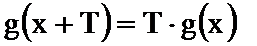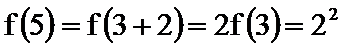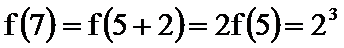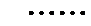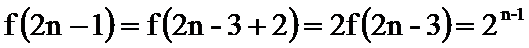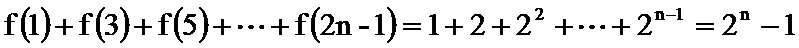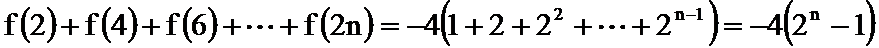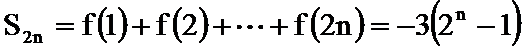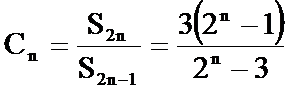- 数列的极限
- 共32题
11. 无穷数列
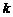
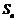
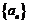
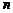
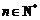
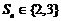
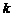
值为___________
正确答案
知识点
8.无穷数列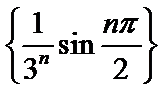
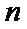
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.计算: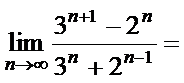
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
3.计算:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.计算:
正确答案
3
解析
分子、分母同除以3n+1,可求得极限为3。
考查方向
本题主要考查了极限的知识
解题思路
本题考查极限,解题步骤如下:利用极限的运算法则求解。
易错点
本题必须注意极限的运算法则。
知识点
18.设




正确答案
解析
知识点
数列
正确答案
:
解析
利用等比数列求和公式


考查方向
本题主要考查了等比数列求和的基本运算
易错点
等比数列的求和公式忘记
知识点
5.无穷等比数列





正确答案
解析
设无穷等比数列






考查方向
本题主要考查了无穷等比数列各项和,考查学生的基础知识掌握能力,属于容易题.
解题思路
先确定公比







易错点
对前




知识点
5.无穷等比数列



则前


正确答案
解析
第一步,先求出等比数列


第二步,因为


考查方向
解题思路
本题应该分为两步,首先求出等比数列



易错点
本题必须注意
(1)只有公比


(2)只有公比



知识点
23.已知函数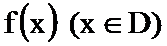
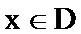
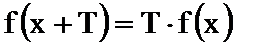
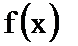
(1)判断
(2)证明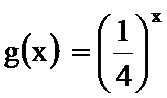
(3)若
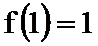
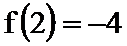
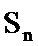
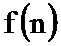
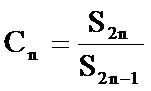
正确答案
(1)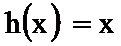
(2)证明略
(3)
解析
解:(1) 设:
则 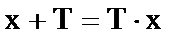
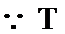
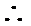
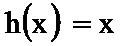
(2) 设:
则 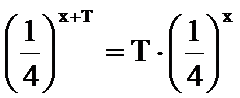
下证唯一性:
若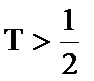
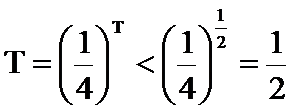
若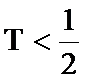
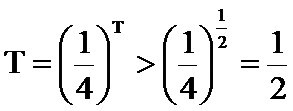
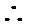
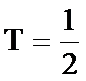
(3)
同理:
同理:
考查方向
解题思路
首先作到最后,要有耐心和信心,认真审题,发掘题目中的可利用信息。第一问直接证明有困难,可以考虑反证法;第三问因为奇数项和偶数项的变化规律不同,宜采用分组求和法。
易错点
第三问数列的奇数项和偶数项要区别对待,忽视容易产生错误。
知识点
扫码查看完整答案与解析