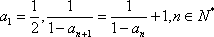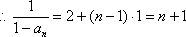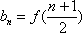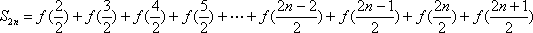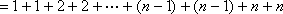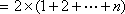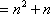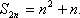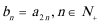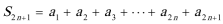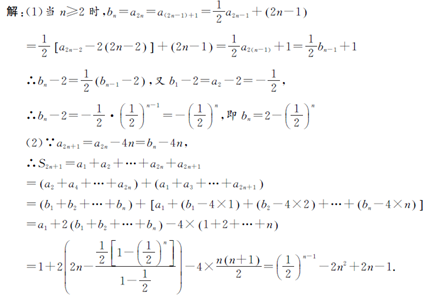- 分组转化法求和
- 共36题
设数列{an}满足:。
(1)求数列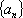
(2)若[

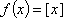
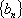
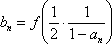
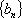
正确答案
见解析。
解析
(1)由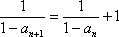
知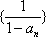

即
(2)
即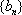
知识点
17.已知Sn为数列{an}的前n项和,且2an=Sn+n.
(1)若bn=an+1,证明:数列{bn}是等比数列;
(2)求数列{Sn}的前n项和Tn。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列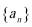
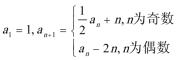
(1)求数列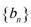
(2)求和
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.等比数列{an}中的前三项a1、a2、a3分别是下面数阵中第一、二、三行中的某三个数,且三个数不在同一列.
(1)求此数列{an}的通项公式;
(2)若数列{bn}满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.数列{an}中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)。
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn;
(3)设

正确答案
解:(1)由an+2=2an+1-an
d=
(2)由an=10-2n≥0可得n≤5,当n≤5时,Sn=-n2+9n,当n>5时,Sn=n2-9n+40,故Sn=
(3)bn=




解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析