- 分组转化法求和
- 共36题
17.在数列



(I)求数列
(II)求数列


(III)证明存在




正确答案
(I)解法一:


由此可猜想出数列

以下用数学归纳法证明.
(1)当

(2)假设当
那么,
这就是说,当
根据(1)和(2)可知,
等式


解法二:由
可得
所以
故
所以数列
(II)
设

当
这时数列

当



(III)通过分析,推测数列

下面证明:
由


所以③式成立.
因此,存在



解析
解析已在路上飞奔,马上就到!
知识点
23.一青蛙从点





(1)若点





(2)若点




(3)若点




正确答案
(1)设
所以

(2) 依题意,
随着

(方法二)∴



又
∴
于是,当
当
∴
解析
解析已在路上飞奔,马上就到!
知识点
21. 









(1)求函数
(2)设

(3)若(2)中数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列

(1) 求证:数列

(2) 求数列


(3) 若数列





正确答案
(1)∵
∴数列

数列


(2)
(3)


所以

∴
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知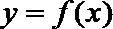
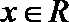
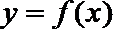
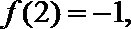
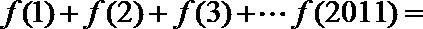
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析















































