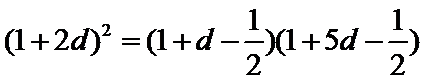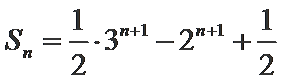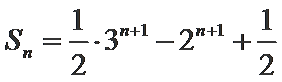- 分组转化法求和
- 共36题
已知等差数列


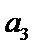
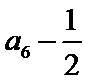
17.求
18.设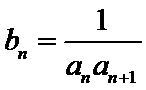
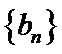

正确答案
(1)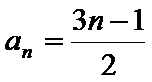
解析
试题分析:本题属查了等差和等比数列及裂项相消法求和,(1)根据已知条件构造方程解出公差d,再求出通项公式;(2)利用裂项相消法求解。
(I)由题意设
得

考查方向
解题思路
本题考查了等差和等比数列及裂项相消法求和,解题步骤如下:(1)根据已知条件构造方程解出公差d,再求出通项公式;(2)利用裂项相消法求解。
易错点
不会利用裂项相消法解题。
正确答案
(2)
解析
试题分析:本题属查了等差和等比数列及裂项相消法求和,(1)根据已知条件构造方程解出公差d,再求出通项公式;(2)利用裂项相消法求解。
(II)
考查方向
解题思路
本题考查了等差和等比数列及裂项相消法求和,解题步骤如下:(1)根据已知条件构造方程解出公差d,再求出通项公式;(2)利用裂项相消法求解。
易错点
不会利用裂项相消法解题。
14.已知数列

正确答案
解析
当n=1时,a1=S1=9;当n≥2时,an=Sn-Sn-1=11-2n,
由于n=1时,a1=9也满足11-2n,
因此an=11-2n.
(1)当n>5时,
(2)当n≤5时,
综合(1)(2),得
知识点
17. 已知数列{


(Ⅰ)求数列{
(Ⅱ)若



正确答案
an=4n-3;
解析
⑴解:由已知条件:






⑵解:由⑴可得





考查方向
本题主要考查数列的综合运算
解题思路
1、求出an;
2、利用公式分类讨论,即可得到结果。
易错点
本题易在分类讨论时发生错误。
知识点
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张.为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列

(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
正确答案
(1)
当


当





(2)当

当
由

即
解得

解析
本题属于数列的应用题,题目的难度是中等,本题的关键是:
(1)、从所给的数列中找出规律,并求出两数列的通项公式;
(2)、再根据数列的通项公式的分段函数性质,求出各自的前n项和,最后利用函数的性质给出答案。这类数列的应用题型较为常见。
考查方向
本题考查了数列与函数之间的综合应用,特别是分段函数与数列的应用
易错点
1、分类讨论:



知识点
20.设数列{an}满足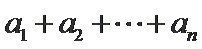
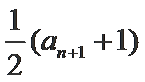
(1)求证数列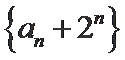
(2)求数列{an}的前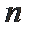
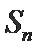
正确答案
(1)略
(2)
解析
(1) 解 由条件可得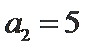
两式相减整理得an+1-3an=2n,则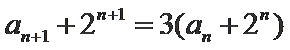
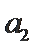
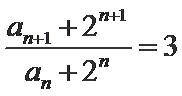
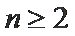
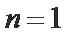
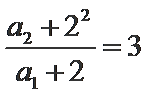
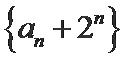
(2)法一:由2Sn=an+1-2n+1+1直接可得
法二:直接求和公式.
考查方向
本题主要考查等比数列的定义以及与之间的关系等知识。
解题思路
利用等式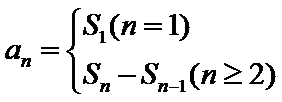
易错点
第一问没有验证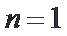
知识点
扫码查看完整答案与解析