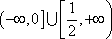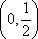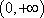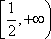- 导数的乘法与除法法则
- 共1249题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知










正确答案
解析
由题意





∴k



又|




∴k-2+(1-2k)·cos
∴k-2=

知识点
在平面直角坐标系xOy中,已知P是函数f(x)=ex(x>0)的图象上的动点,该图象在点P处的切线l交y轴于点M.过点P作l的垂线交y轴于点N.设线段MN的中点的纵坐标为t,则t的最大值是________.
正确答案

解析
设P(x0,
∴点P处的切线l,其斜率为f ′(x0)=

∴直线l的方程为
直线l′的方程为
由题意
令
∴当x0<1时, g ′(x0)>0,函数g(x0)为增函数。
当x0>1时, g ′(x0)<0,函数g(x0)为减函数。
∴g(x0)在x0=1处取极大值,亦即x0>0时t的最大值。
知识点
已知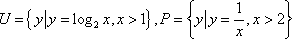
正确答案
解析
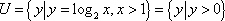
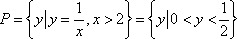
故 
知识点


正确答案
17
解析






知识点
已知椭圆

(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足

(2)设直线








(3)对于椭圆









正确答案
见解析。
解析
(1) 
(2) 由方程组

因为直线



所以>0,即
设C(x1,y1)、D(x2,y2),CD中点坐标为(x0,y0),
则
由方程组
又因为

故E为CD的中点;
(3) 求作点P1、P2的步骤:1求出PQ的中点
2求出直线OE的斜率
3由

4从而得直线CD的方程:
5将直线CD与椭圆Γ的方程联立,方程组的解即为点P1、P2的坐标。
欲使P1、P2存在,必须点E在椭圆内,
所以


又0< <,即

故 的取值范围是
知识点
曲线y=xex﹣1在点(1,1)处切线的斜率等于( )
正确答案
解析
函数的导数为f′(x)=ex﹣1+xex﹣1=(1+x)ex﹣1,
当x=1时,f′(1)=2,
即曲线y=xex﹣1在点(1,1)处切线的斜率k=f′(1)=2,
故选:C。
知识点
如图4, 



(1)
正确答案
(1)
解析
(1)由几何概型概率计算公式可得
(2)由条件概率的计算公式可得
知识点
扫码查看完整答案与解析