导数的乘法与除法法则
共1249题

· 导数的乘法与除法法则

导数的乘法与除法法则
共1249题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 10 分

在平面直角坐标系中，已知，，，，其中，设直线与的交点为，求动点的轨迹的参数方程（以为参数）及普通方程。

正确答案

见解析。

解析

直线的方程为， ①

直线的方程为， ②

由①②解得，动点的轨迹的参数方程为（为参数，且），

将平方得， ③

将平方得， ④

由③④得，。

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 10 分

设且，证明：

。

正确答案

见解析。

解析

（1）当时，有，命题成立。

（2）假设当时，命题成立，

即

成立，

那么，当时，有

。

所以当时，命题也成立。

根据（1）和（2），可知结论对任意的且都成立。

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 10 分

下图是某游戏中使用的材质均匀的圆形转盘，其中Ⅰ，Ⅱ，Ⅲ，Ⅳ部分的面积各占转盘面积的，，，。

游戏规则如下：

① 当指针指到Ⅰ，Ⅱ， Ⅲ，Ⅳ部分时，分别获得积分100分，40分，10分，0分；

② （ⅰ）若参加该游戏转一次转盘获得的积分不是40分，则按①获得相应的积分，游戏结束；

（ⅱ）若参加该游戏转一次获得的积分是40分，则用抛一枚质地均匀的硬币的方法来决定是否继续游戏，正面向上时，游戏结束；反面向上时，再转一次转盘，若再转一次的积分不高于40分，则最终积分为0分，否则最终积分为100分，游戏结束。

设某人参加该游戏一次所获积分为。

（1）求的概率；

（2）求的概率分布及数学期望。

正确答案

见解析。

解析

（1）事件“”包含：“首次积分为0分”和“首次积分为40分

后再转一次的积分不高于40分”，且两者互斥，

所以；

（2）的所有可能取值为0，10，40，100，

由（1）知，

又，

，

所以的概率分布为：

因此，。

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 10 分

等差数列满足.

（1）设数列的公差，为数列的第项的值，求证：的展开式中不含常数项；

（2）设数列的公差为正整数，为数列的第项的值，求公差的值的集合，使得对于一切，的展开式中均不含常数项。

正确答案

见解析。

解析

（1），展开式，则，即，，

所以的展开式中不含常数项.

（2），展开式

则，即，

① 若，

② 若，，易知时，为自然数

③ 若，，易知时，为自然数

综上，公差的值的集合为

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 12 分

某研究机构准备举行一次数学新课程研讨会，共邀请50名一线教师参加，使用不同版

本教材的教师人数如下表所示：

（1）从这50名教师中随机选出2名，求2人所使用版本相同的概率；

（2）若随机选出2名使用人教版的教师发言，设使用人教A版的教师人数为，求随机变量的分布列和数学期望。

正确答案

见解析

解析

解析：（1）从50名教师随机选出2名的方法数为，选出2人使用版本相同的方法数为，故2人使用版本相同的概率为.

（2）的所有可能取值为0，1，2. ，， .∴的分布列为

∴.

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 14 分

设函数.

（1）求函数的最小值；

（2）设，讨论函数的单调性；

（3）斜率为的直线与曲线交于、两点，求证：.

正确答案

见解析

解析

解析：（1），令，得.∵当时，；当时，，∴当时，.

（2），.

① 当时，恒有，在上是增函数；

② 当时，令，得，解得；令，得，解得. 综上，当时，在上是增函数；当时，在上单调递增，在上单调递减.

（3）证：. 要证，即证，等价于证，令，则只要证，由知，故等价于证 (*).

① 设，则，故在上是增函数，

∴ 当时，，即.

② 设，则，故在上是增函数，

∴ 当时，，即.由①②知(*)成立，得证.

知识点

导数的乘法与除法法则

题型：单选题

单选题 · 5 分

已知与为互相垂直的单位向量，，且与的夹角为锐角，则实数的取值范围是

正确答案

解析

注意到与的夹角为锐角，故，且注意到时，

知识点

导数的乘法与除法法则

题型：单选题

单选题 · 5 分

已知某几何体的侧视图与其正视图相同，相关的尺寸如下图所示，则这个几何体的体积是（）

C `

正确答案

解析

依题意该几何体为一空心圆柱，故其体积，选D。

知识点

导数的乘法与除法法则

题型：填空题

填空题 · 5 分

已知函数是定义在区间上的奇函数，则_______。

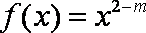
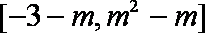
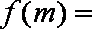
正确答案

解析

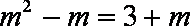
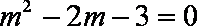
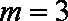
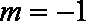
由已知必有，即，∴，或；

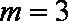
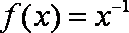
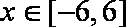
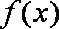
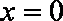
当时，函数即，而，∴在处无意义，故舍去；

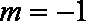
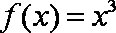
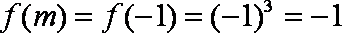
当时，函数即，此时，∴。

知识点

导数的乘法与除法法则

题型：单选题

单选题 · 5 分

已知双曲线（a＞0，b＞0）的两个焦点为、，点A在双曲线第一象限的图象上，若△的面积为1，且，，则双曲线方程为

正确答案

解析

设由已知可求得，从而，由焦点三角形面积得，

知识点

导数的乘法与除法法则

继续学习学习下一知识点

下一知识点 : 简单复合函数的导数

百度题库 > 高考 > 理科数学 > 导数的乘法与除法法则

扫码查看完整答案与解析