导数的乘法与除法法则
共1249题

· 导数的乘法与除法法则

导数的乘法与除法法则
共1249题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

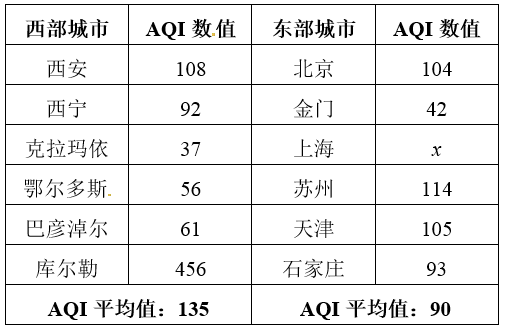
国家环境标准制定的空气质量指数（简称AQI）与空气质量等级对应关系如下表：

下表是由天气网获得的全国东西部各6个城市2015年3月某时刻实时监测到的数据：

（1）求x的值，并根据上表中的统计数据，判断东、西部城市AQI数值的方差的大小关系（只需写出结果）；

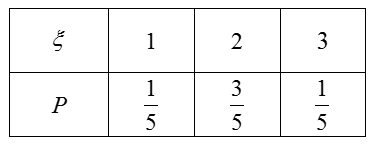
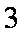
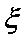
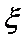
（2）环保部门从空气质量“优”和“轻度污染”的两类城市随机选取个城市组织专家进行调研，记选到空气质量“轻度污染”的城市个数为，求的分布列和数学期望。

正确答案

见解析

解析

解析：

（1）x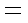82 ………………2分

D东部<D西部 ………………4分

（2）“优”类城市有2个，“轻度污染”类城市有4个。

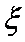
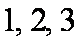
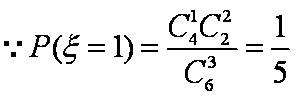
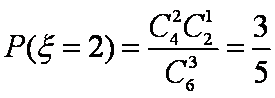
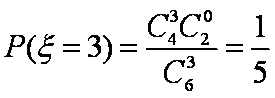
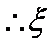
根据题意的所有可能取值为：。 ………………5分

,，。 …11分

的分布列为：

所以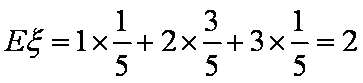。 ………………13分

知识点

导数的乘法与除法法则

题型：单选题

单选题 · 5 分

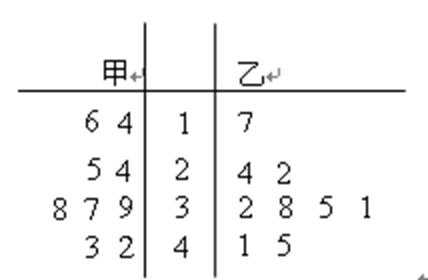
下图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，则甲、乙两人这几场比赛得分的中位数之和是（）

A68

B70

C69

D71

正确答案

解析

甲的中位数为37，乙的中位数为32，所以甲乙两人的中位数之和为37+32=69，选C.

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 10 分

已知曲线：

（1）将曲线绕坐标原点逆时针旋转后，求得到的曲线的方程；

（2）求曲线的焦点坐标和渐近线方程。

正确答案

见解析。

解析

（1）由题设条件，，

，即有，

解得，代入曲线的方程为。

所以将曲线绕坐标原点逆时针旋转后，得到的曲线是。

（2）由（1）知，只须把曲线的焦点、渐近线绕坐标原点顺时针旋转后，即可得到曲线的焦点坐标和渐近线方程。

曲线的焦点坐标是，渐近线方程，

变换矩阵

，，

即曲线的焦点坐标是。而把直线要原点顺时针旋转恰为轴与轴，因此曲线的渐近线方程为和。

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 10 分

如图，是圆的切线，切点为，是过圆心的割线且交圆于点，过作的切线交于点。

求证：（1）；

（2）。

正确答案

见解析。

解析

（1）∵是圆的切线，∴，

连结，则，

∵是圆的切线，∴，

又，∴，∴，则，

而，∴，∴，

（2）将代入得，故，

知识点

导数的乘法与除法法则

题型：单选题

单选题 · 5 分

一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的（）

A外接球的半径为

B表面积为

C体积为

D外接球的表面积为

正确答案

解析

由三视图可知，这是侧面,高的三棱锥，,所以三棱锥的体积为，设外接球的圆心为O半径为，则，在直角三角形中，,即，整理得，解得半径，所以外接球的表面积为，所以A,C,D都不正确，选B.

知识点

导数的乘法与除法法则

题型：单选题

单选题 · 5 分

定义在（-1,1）上的函数f(x)满足：；当时，有；若, ；则P,Q,R的大小关系为

AR>Q>P

BP>R>Q

CR>P>Q

D不能确定

正确答案

解析

∵函数f(x)满足：；当时，有；

∴f(x)在(-1,1)为奇函数,单调减函数,且在(-1,0)时,f(x)>0,在(0,1)时f(x)<0;

∴R＝f(0)=0, <0<R,

∵,

∴

=Q->Q

P=<0<R,故选C

知识点

导数的乘法与除法法则

题型：单选题

单选题 · 5 分

如图是函数在一个周期内的图象，则阴影部分的面积是（）

正确答案

解析

函数的周期，.阴影部分面积为:

.选B.

知识点

导数的乘法与除法法则

题型：单选题

单选题 · 5 分

已知集合,,如果,则等于（）

A-1

B-2

C-2或-1

正确答案

解析

,因为，所以或，选C.

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 12 分

已知在等比数列中，，数列满足.

（1）求数列的通项公式；

（2）设数列的前项和为，若，恒成立，求的取值范围.

正确答案

见解析

解析

（1）设公比为，则.

.……………………2分

时，.

∴…………………5分

（2），，

两式相减得：.

∴时，；

时，，，

两式相减得：.

∴,有.…………………7分

记，则，

∴，

∴数列递增，其最小值为.

故.………………12分

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 12 分

如图1，是直角△斜边上的高，沿把△的两部分折成直二面角（如图2），于.

（1）证明：；

（2）设，与平面所成的角为，二面角的大小为，求证：；

（3）设，为的中点，在线段上是否存在一点，使得∥平面?若存在，求的值；若不存在，请说明理由。

正确答案

见解析

解析

（1）∵，∴是二面角的平面角.又∵二面角是直二面角，∴,∴平面，∴，又，∴平面，∴.…………………………………4分

（2）由（1）

又，

∴.………………………8分

（3）连接交于点，连接,则∥.

∵,∴,∴为的中点，

而为的中点，∴为的重心,

∴,∴.

即在线段上是否存在一点，使得∥，

此时.……………………12分

知识点

导数的乘法与除法法则

继续学习学习下一知识点

下一知识点 : 简单复合函数的导数

百度题库 > 高考 > 理科数学 > 导数的乘法与除法法则

扫码查看完整答案与解析