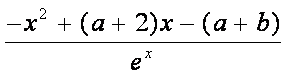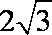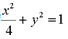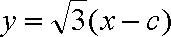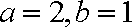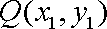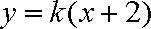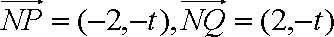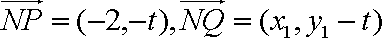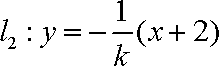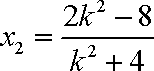- 导数的乘法与除法法则
- 共1249题
如题是收集重庆市2013年的9月和气象才几点处的平均气温,(单位:
正确答案
解析
解析:由图可知,平均气温在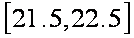
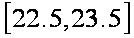
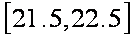
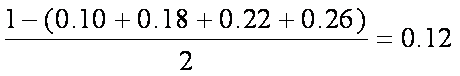
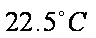
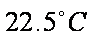
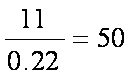
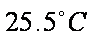
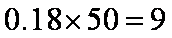
故选:D
知识点
已知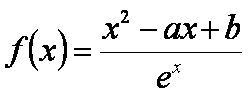
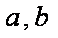
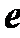
(1)若曲线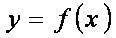
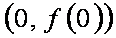

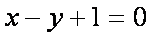
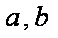
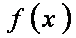
(2)已知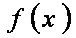
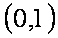
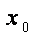
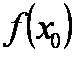
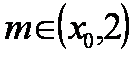
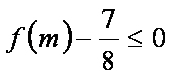
正确答案
见解析
解析
(1)f ′ (x)=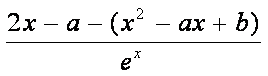
因f (x)在点(0, f (0))处的切线方程为x-y+1=0,有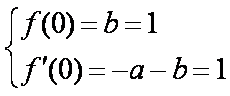
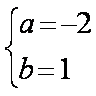
所以f ′ (x)=-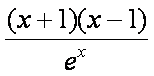
同理,f (x
(2)由f (x)在区间 (0,1) 上有且仅有一个极值点x0,且f (x0)为极大值,可知

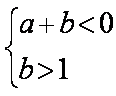
而f (2)=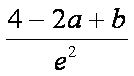
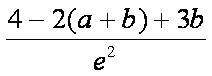
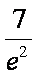
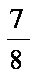
由f (x)在(x0, 2)上单调递减,则对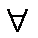
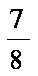
故不存在m∈(x0, 2),使f (m)-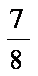
知识点
已知i是虚数单位,则
正确答案
解析
解:

知识点
直线

正确答案
解析
根据题意画出图形,如图所示:
在Rt△AOB中,由|OA|=2,|OB|=2
根据勾股定理得:|AB|=
∵OA=
∴∠BAO=60°,又OA=OC,
∴△AOC为等边三角形,
∴∠AOC=60°,又圆O的半径OA=2,
∴



故答案为:
知识点
已知抛物线y=ax2(a∈R)的准线方程为y=﹣1,则a= _________ 。
正确答案
解析
抛物线y=ax2的标准方程为 x2=





知识点
已知




(1)求角
(2)若向量

正确答案
(1)
解析
解析:(1)由题意得
即
由余弦定理得

(2)


所以

知识点
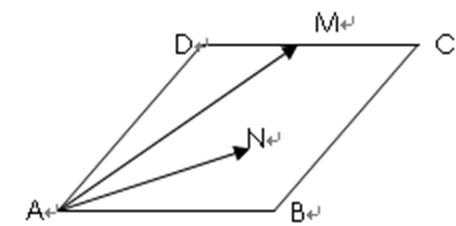
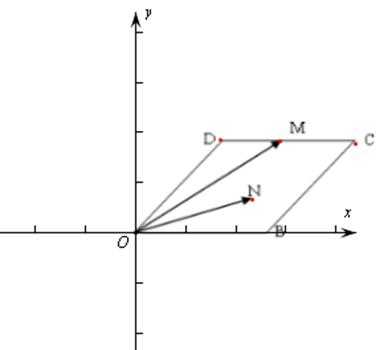
如图,菱形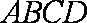
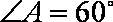
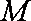
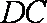
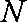
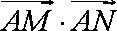
正确答案
解析
以A点为坐标原点,建立直角坐标系,因为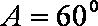
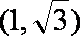
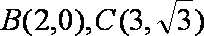
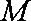
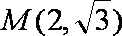
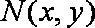
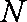
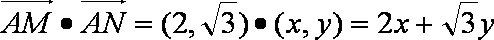
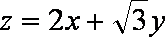
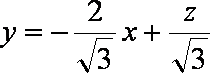
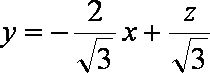
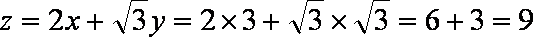
知识点
设

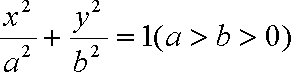
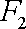


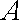
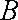
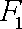
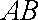


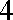
(1)求椭圆
(2)过椭圆
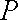
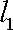

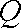
(ⅰ)若点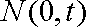

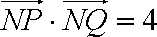
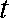
(ⅱ)过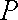
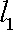
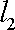


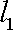
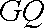

正确答案
(1)
(2)(ⅰ)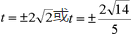
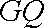

解析
解析:(1)设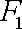
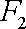
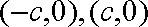
由题意得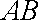
因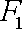
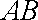

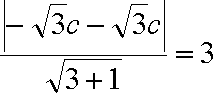
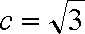
所以有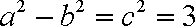
由题意知: 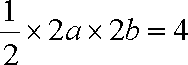
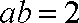
联立①②解得:
所求椭圆
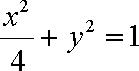
(2)由(1)知: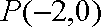
根据题意可知直线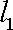
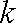
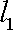
把它代入椭圆
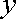
由韦达定理得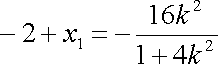
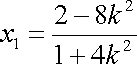
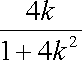
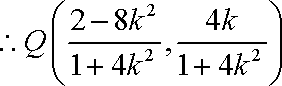

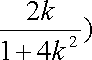
(ⅰ)当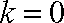
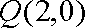

于是
由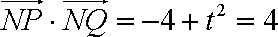
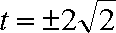
当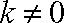

因为点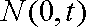

令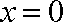
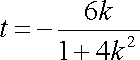
由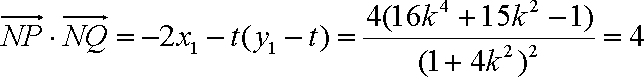
代入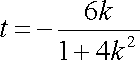
综上, 满足条件的实数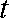
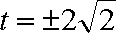
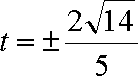
(ⅱ)设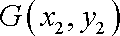
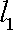
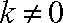
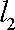
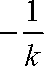
由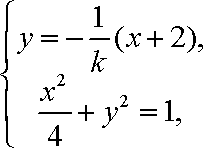
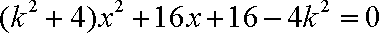
∵此方程有一根为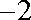
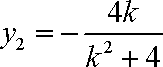
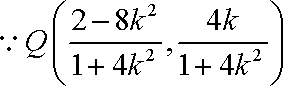
所以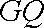
令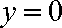
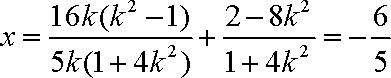
所以直线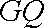

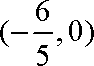
知识点
阅读右侧程序框图,则输出的数据
正确答案
0
解析
第一次运算,





知识点
设正项数列




(1)求
(2)求证:
正确答案
见解析
解析
(1)由




相减有

又n=2时,





则有an+1-an=1(n≥1),且a1=

(2)由(1),Sn=



令f (x)=x-ln(1+x) (x


故f (x)在(0,+∞)单调递增,f (x)>f (0)=0,所以ln(1+x)<x (x>0),
故ln bn+1=ln bn+





ln bn+1-ln bn<



故ln bn+1 =(ln bn+1-ln bn)+(ln bn-ln bn-1)+…+(ln b2-ln b1)
<










=









即ln bn+1<

当n=1时,b1<e2,故bn<e2。
知识点
扫码查看完整答案与解析