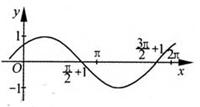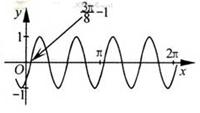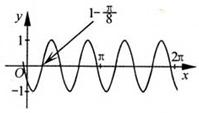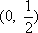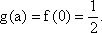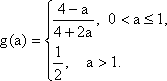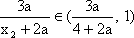- 导数的乘法与除法法则
- 共1249题
已知函数

正确答案
解析
得:


知识点
双曲线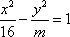

正确答案
9
解析
由双曲线方程知a=4.又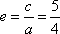
知识点
把函数y=cos2x+1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是
正确答案
解析
把函数y=cos2x+1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)得:y1=cosx+1,向左平移1个单位长度得:y2=cos(x—1)+1,再向下平移1个单位长度得:y3=cos(x—1),令x=0,得:y3>0;x=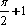
知识点
已知
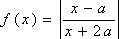
(1)记

(2)是否存在
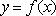
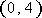

正确答案
(1)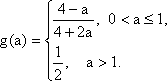
解析
(1)当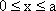
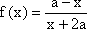
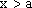
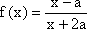
当
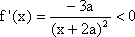
当
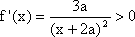

① 若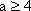
② 若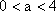
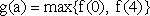
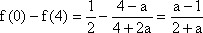
当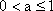
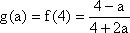
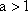
综上所述,
(2) 由(I)可知,若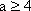
当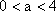
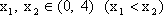
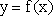
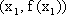
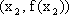
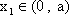
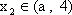
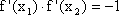
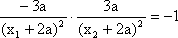
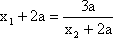
由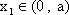
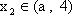
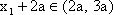
故(*)成立等价于集合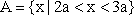
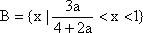
因为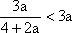
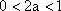
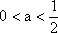
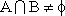
综上所述,存在
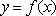

知识点
如图,



延长









正确答案

解析






知识点
“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的( )。
正确答案
解析
解析:函数f(x)的图象有以下三种情形:


a=0 a>0 a<0
由图象可知f(x)在区间(0,+∞)内单调递增时,a≤0,故选C.
知识点
在如图所示的锐角三角形空地中,欲建一个面积不小于300 m2的内接矩形花园(阴影部分),则其边长x(单位:m)的取值范围是( )。
正确答案
解析
设矩形另一边长为y,如图所示.
知识点
设椭圆E:
(1)若椭圆E的焦距为1,求椭圆E的方程;
(2)设F1,F2分别是椭圆E的左、右焦点,P为椭圆E上第一象限内的点,直线F2P交y轴于点Q,并且F1P⊥F1Q.证明:当a变化时,点P在某定直线上。
正确答案
见解析
解析
(1)因为焦距为1,所以2a2-1=
解得a2=
故椭圆E的方程为
(2)设P(x0,y0),F1(-c,0),F2(c,0),其中
由题设知x0≠c,
则直线F1P的斜率

直线F2P的斜率

故直线F2P的方程为y=
当x=0时,y=
即点Q坐标为
因此,直线F1Q的斜率为

由于F1P⊥F1Q,
所以

化简得
将①代入椭圆E的方程,由于点P(x0,y0)在第一象限,解得x0=a2,y0=1-a2,即点P在定直线x+y=1上。
知识点
已知a>0,b

(1)证明:当0≤x≤1时,
1)函数
2) 
(2) 若﹣1≤

正确答案
见解析
解析
本题主要考察不等式,导数,单调性,线性规划等知识点及综合运用能力。
(1)
1)
当b≤0时,
此时

当b>0时,
此时

综上所述:函数
2) 要证


亦即证
∵

当b≤0时,
此时

当b<0时,
≤|2a-b|﹢a;
综上所述:函数
即
(2)由(1)知:函数
且函数
∵﹣1≤

∴|2a-b|﹢a≤1。
取b为纵轴,a为横轴。
则可行域为:

作图如下:
由图易得:当目标函数为z=a+b过P(1,2)时,有
∴所求a+b的取值范围为:
知识点
设函数
(1)若

(2)若当


正确答案
见解析。
解析
(1)当


当



故


(2)
由(1)知
故




而


由



从而当

故当




综合得

知识点
扫码查看完整答案与解析